3 2/3 X 2 3/4 As A Fraction
listenit
May 24, 2025 · 5 min read
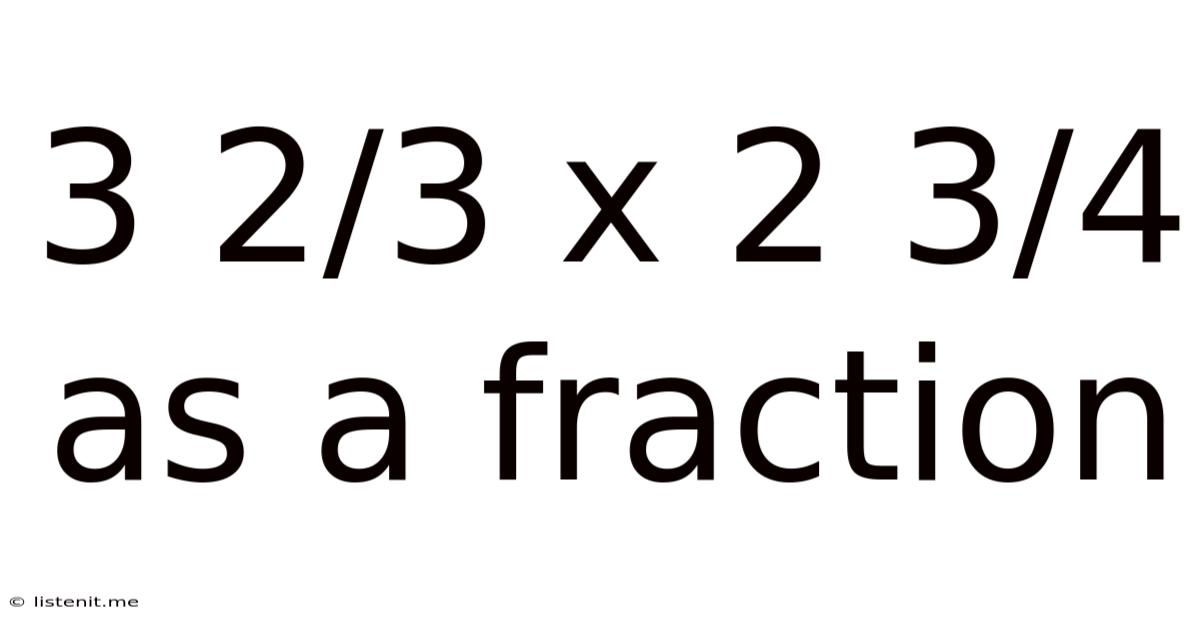
Table of Contents
3 2/3 x 2 3/4 as a Fraction: A Comprehensive Guide
Multiplying mixed numbers can seem daunting, but with a systematic approach, it becomes straightforward. This guide will walk you through the process of calculating 3 2/3 x 2 3/4 as a fraction, explaining each step in detail and providing additional insights to enhance your understanding of fraction multiplication.
Understanding Mixed Numbers and Improper Fractions
Before tackling the multiplication, let's review the fundamentals. A mixed number combines a whole number and a fraction (e.g., 3 2/3). An improper fraction, on the other hand, has a numerator larger than or equal to its denominator (e.g., 11/3). These two forms are interchangeable. Converting between them is crucial for efficient fraction multiplication.
Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: In 3 2/3, multiply 3 (whole number) by 3 (denominator) = 9.
- Add the numerator: Add the result (9) to the numerator (2) = 11.
- Keep the same denominator: The denominator remains 3.
Therefore, 3 2/3 as an improper fraction is 11/3.
Let's apply this to 2 3/4:
- Multiply the whole number (2) by the denominator (4) = 8.
- Add the numerator (3) to the result (8) = 11.
- Keep the denominator (4).
Thus, 2 3/4 becomes 11/4.
Multiplying Improper Fractions
Now that we've converted our mixed numbers into improper fractions, we can proceed with the multiplication:
11/3 x 11/4
Multiplying fractions is simpler than adding or subtracting them. We simply multiply the numerators together and the denominators together:
(11 x 11) / (3 x 4) = 121/12
Converting the Result Back to a Mixed Number (Optional)
While 121/12 is a perfectly acceptable answer, it's often preferred to express the result as a mixed number for better readability. To do this, perform long division:
121 ÷ 12 = 10 with a remainder of 1
The quotient (10) becomes the whole number part, and the remainder (1) becomes the numerator of the fraction. The denominator remains the same (12). Therefore, 121/12 as a mixed number is 10 1/12.
Alternative Methods and Considerations
While the above method is the most common and straightforward, there are alternative approaches you can use, especially if you're comfortable with factoring. Let's explore some of them.
Factoring Before Multiplication
Before multiplying the numerators and denominators directly, you can simplify the calculation by identifying common factors in the numerators and denominators. This is called canceling. However, in this particular case (11/3 x 11/4), there are no common factors between the numerators and denominators that can be cancelled. This means the direct multiplication approach is the most efficient here.
Distributive Property (Less Efficient in this Case)
The distributive property can sometimes be applied to simplify multiplication of mixed numbers, but it's generally less efficient than converting to improper fractions first. Let's illustrate why:
Applying the distributive property would involve expanding the expression:
(3 + 2/3) x (2 + 3/4)
This would lead to four separate multiplications:
(3 x 2) + (3 x 3/4) + (2/3 x 2) + (2/3 x 3/4)
While this method works, it’s significantly more time-consuming and prone to errors compared to the direct conversion to improper fractions and then multiplying.
Practical Applications and Real-World Examples
Understanding how to multiply mixed numbers has many practical applications in various fields. Consider these examples:
- Baking and Cooking: Recipes often require precise measurements. If a recipe calls for 2 1/2 cups of flour and you want to double the recipe, you'll need to multiply 2 1/2 by 2.
- Construction and Carpentry: Calculating the area of a room or the amount of material needed for a project often involves multiplying mixed numbers representing dimensions.
- Sewing and Quilting: Cutting fabric for a project often involves precise measurements and calculations with fractions and mixed numbers.
- Financial Calculations: Interest calculations, calculating discounts, or figuring out portions of a budget can involve working with fractions and mixed numbers.
Troubleshooting Common Mistakes
When working with mixed numbers and fractions, several common errors can occur:
- Incorrect conversion to improper fractions: Ensure you're accurately multiplying the whole number by the denominator and adding the numerator before keeping the original denominator.
- Forgetting to simplify: Always simplify your answer to its lowest terms if possible, especially when expressing the result as a fraction.
- Errors in multiplication: Double-check your multiplication of numerators and denominators to avoid simple calculation errors.
- Incorrect conversion back to mixed number: When converting back to a mixed number, ensure you correctly identify the quotient and the remainder.
Advanced Techniques and Further Exploration
While this guide focuses on a basic calculation, the principles discussed apply to more complex problems involving multiplication of multiple mixed numbers or combinations of mixed numbers and other fractions. Practice is key to mastering these skills.
You can explore more complex problems to hone your skills. For example, try calculating:
- (1 1/2) x (2 2/3) x (3 1/4)
- (4 3/5) x (1 1/2) x (2 1/3)
Remember, breaking down the problem into manageable steps—converting mixed numbers to improper fractions, multiplying, simplifying, and converting back to a mixed number (if needed)—will help you approach even the most complex calculations with confidence.
Conclusion
Multiplying mixed numbers, such as 3 2/3 x 2 3/4, might seem intimidating at first, but by systematically converting mixed numbers to improper fractions, performing the multiplication, and simplifying the result, the process becomes quite straightforward. This comprehensive guide has not only shown you the solution (10 1/12) but also equipped you with the necessary knowledge and techniques to handle similar calculations with confidence and efficiency. Remember to practice regularly to improve your skills and understanding of fraction operations.
Latest Posts
Latest Posts
-
What Percent Is 20 Out Of 23
May 25, 2025
-
11 Out Of 17 As A Percentage
May 25, 2025
-
How Many Days Away Is March 7
May 25, 2025
-
What Is The Prime Factorization Of 71
May 25, 2025
-
What Is The Greatest Common Factor Of 48 And 42
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 2/3 X 2 3/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.