26 Is What Percent Of 65
listenit
May 12, 2025 · 4 min read
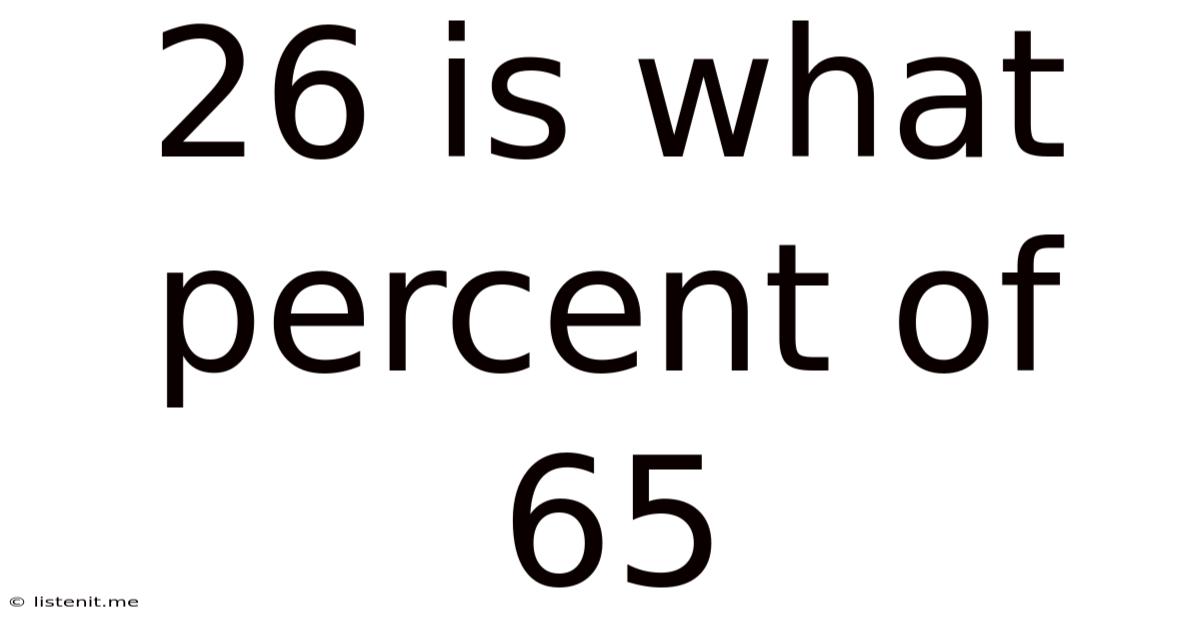
Table of Contents
26 is What Percent of 65? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific analyses. This comprehensive guide will not only answer the question, "26 is what percent of 65?" but will also equip you with the knowledge and strategies to confidently tackle any percentage problem. We'll delve into the calculation itself, explore different methods, and provide practical applications to solidify your understanding.
Calculating the Percentage: The Step-by-Step Approach
The core of percentage calculation involves understanding the relationship between a part and a whole. In our case, 26 is the "part," and 65 is the "whole." To find the percentage, we follow these simple steps:
-
Divide the part by the whole: This gives us the decimal equivalent of the percentage. In our example: 26 / 65 = 0.4
-
Multiply the decimal by 100: This converts the decimal to a percentage. Continuing our example: 0.4 * 100 = 40
-
Add the percentage symbol: This signifies that the result represents a percentage. Therefore, 26 is 40% of 65.
Alternative Methods: Flexibility in Calculation
While the above method is straightforward, several alternative approaches can be used, depending on your preference and the complexity of the problem.
Method 2: Using Proportions
Proportions offer a visual and intuitive way to solve percentage problems. We set up a proportion as follows:
- Part / Whole = Percentage / 100
Substituting our values:
- 26 / 65 = x / 100
To solve for x (the percentage), we cross-multiply:
- 26 * 100 = 65 * x
- 2600 = 65x
- x = 2600 / 65
- x = 40
Therefore, 26 is 40% of 65. This method highlights the proportional relationship between the parts and the whole.
Method 3: Using a Calculator
Calculators are invaluable tools for quick and accurate percentage calculations. Most calculators have a percentage function (%) that simplifies the process. Simply enter "26 ÷ 65 = %" to directly obtain the result: 40%. This method is efficient for quick calculations, particularly with more complex numbers.
Understanding the Concept of Percentage
A percentage is simply a fraction expressed as a part of 100. It represents a proportion or rate per hundred. The symbol "%" signifies "per hundred" or "out of 100." Understanding this fundamental concept is key to mastering percentage calculations.
For example, 40% can be expressed as:
- 40/100
- 0.4 (decimal form)
- 2/5 (simplified fraction)
All these representations convey the same proportional value.
Practical Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple mathematical exercises. Its applications are widespread and crucial in various real-world scenarios:
1. Finance and Budgeting:
- Calculating discounts: Determining the final price after a percentage discount (e.g., a 20% off sale).
- Analyzing interest rates: Understanding the interest accrued on loans or investments.
- Tracking expenses: Calculating the percentage of income spent on different categories.
- Calculating taxes: Determining the tax amount based on a percentage of income or purchase price.
2. Business and Economics:
- Market share analysis: Determining the percentage of market share held by a company.
- Profit margin calculation: Calculating the percentage of profit relative to revenue.
- Growth rate analysis: Measuring the percentage increase or decrease in sales or profits over time.
- Investment returns: Calculating the percentage return on investment.
3. Science and Statistics:
- Data representation: Presenting data as percentages in charts and graphs for easier understanding.
- Probability and statistics: Expressing probabilities and statistical significance as percentages.
- Experimental results: Analyzing experimental data and representing the results as percentages.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant.
- Understanding sales tax: Knowing the total cost after sales tax is added.
- Comparing prices: Determining the percentage difference between two products.
Beyond the Basics: Tackling More Complex Problems
While our initial problem was straightforward, percentage calculations can become more complex. Here are some examples and approaches to solve them:
Calculating Percentage Increase or Decrease:
To calculate a percentage increase or decrease, you need the initial value and the final value. The formula is:
(Final Value - Initial Value) / Initial Value * 100%
For example, if a product's price increased from $50 to $60, the percentage increase is:
($60 - $50) / $50 * 100% = 20%
Finding the Original Value:
If you know the percentage and the final value (after a percentage increase or decrease), you can work backward to find the original value.
For example, if a product is currently priced at $72 after a 20% increase, the original price can be calculated as follows:
Let x be the original price. Then:
x + 0.20x = $72 1.20x = $72 x = $72 / 1.20 x = $60
The original price was $60.
Percentage of a Percentage:
Calculating a percentage of a percentage involves multiplying the percentages together and then applying the result to the base value.
For example, finding 25% of 50% of 100:
0.25 * 0.50 * 100 = 12.5
Mastering Percentages: A Path to Numerical Fluency
This comprehensive guide has demonstrated that calculating percentages, even seemingly simple problems like "26 is what percent of 65?", involves understanding the underlying concepts and applying different methods. By mastering these fundamental principles, you gain valuable skills applicable to diverse areas of life. Practice is crucial—the more you work with percentage problems, the more comfortable and efficient you'll become. Remember that understanding the underlying principles, exploring alternative methods, and practicing regularly will lead to numerical fluency and confidence in tackling any percentage-related challenge.
Latest Posts
Latest Posts
-
Found In Animal Cells But Not Plant Cells
May 12, 2025
-
What Is Prime Factorization Of 84
May 12, 2025
-
Why Are Lanthanides And Actinides Separated From The Periodic Table
May 12, 2025
-
Find X To The Nearest Tenth
May 12, 2025
-
What Is The Molecular Geometry Of N2
May 12, 2025
Related Post
Thank you for visiting our website which covers about 26 Is What Percent Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.