25 Of What Number Is 2
listenit
May 10, 2025 · 4 min read
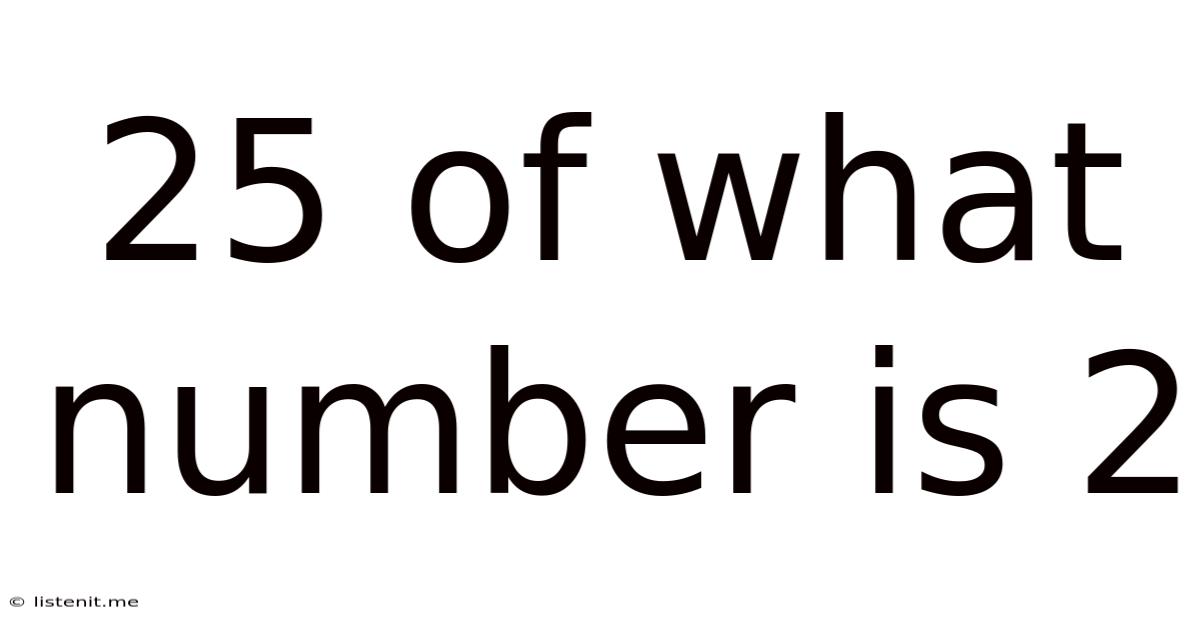
Table of Contents
25% of What Number is 2? Unraveling the Mystery of Percentages
Finding a missing number in a percentage problem might seem daunting at first glance, but with a systematic approach, it becomes surprisingly straightforward. This article delves into the question, "25% of what number is 2?" We'll not only solve this specific problem but also equip you with the knowledge and tools to tackle any similar percentage calculation confidently. We'll explore various methods, from basic arithmetic to utilizing the power of algebraic equations, ensuring a comprehensive understanding of percentage calculations.
Understanding Percentages: The Foundation
Before we dive into solving our problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For instance, 25% can be written as 25/100 or 0.25 as a decimal. This simple equivalence is the key to unlocking percentage problems.
Key Concepts:
- Percent: The word "percent" literally means "per hundred."
- Fraction: A percentage can always be represented as a fraction with a denominator of 100.
- Decimal: A percentage can also be written as a decimal by dividing the percentage by 100.
Method 1: Using Proportions
The proportion method offers an intuitive and easy-to-understand approach to solving percentage problems. We set up a proportion, equating two ratios. In our case:
- 25/100 = 2/x
Where:
- 25/100 represents 25%
- 2 is the given part
- x is the unknown whole number we're trying to find.
To solve for x, we cross-multiply:
25 * x = 100 * 2
25x = 200
Now, divide both sides by 25:
x = 200 / 25
x = 8
Therefore, 25% of 8 is 2.
Method 2: Converting Percentage to Decimal
This method involves converting the percentage to its decimal equivalent before performing the calculation.
-
Convert the percentage to a decimal: 25% = 0.25
-
Set up the equation: 0.25 * x = 2
-
Solve for x: Divide both sides of the equation by 0.25:
x = 2 / 0.25
x = 8
Again, we arrive at the solution: 25% of 8 is 2.
Method 3: Using the Formula
A more formal approach involves using the standard percentage formula:
Part = Percentage * Whole
In our problem:
- Part = 2
- Percentage = 25% or 0.25
- Whole = x (what we need to find)
Substituting these values into the formula:
2 = 0.25 * x
Solving for x:
x = 2 / 0.25
x = 8
This confirms our earlier results: 25% of 8 is 2.
Method 4: Algebraic Approach
We can express the problem algebraically. Let's represent the unknown number as 'x'. The problem can be written as:
0.25x = 2
Solving for x:
x = 2 / 0.25
x = 8
Expanding the Understanding: Variations and Applications
While we've solved "25% of what number is 2?", the techniques learned are applicable to a wide range of percentage problems. Let's explore some variations:
Finding the Percentage:
What if the question was, "2 is what percent of 8?" We'd use the formula:
Percentage = (Part / Whole) * 100
Percentage = (2 / 8) * 100 = 25%
Finding the Part:
If the question was, "What is 25% of 8?", we would simply multiply:
Part = 0.25 * 8 = 2
Real-World Applications of Percentage Calculations
Percentage calculations are indispensable in numerous real-world scenarios:
- Finance: Calculating interest, discounts, taxes, and profit margins.
- Retail: Determining sale prices, markups, and profit percentages.
- Science: Representing data in graphs and charts, expressing experimental results.
- Everyday Life: Calculating tips, splitting bills, and understanding statistics.
Troubleshooting Common Errors
Many errors in percentage calculations stem from misunderstanding the relationship between the parts and the whole. Here are some common mistakes to avoid:
- Incorrect Decimal Conversion: Ensure accurate conversion of percentages to decimals.
- Mixing up Parts and Wholes: Clearly identify the part and the whole in the problem.
- Incorrect Order of Operations: Follow the correct order of operations (PEMDAS/BODMAS).
- Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple steps.
Advanced Percentage Problems
Let's consider slightly more complex scenarios to further solidify your understanding:
Example 1: A store offers a 15% discount on an item originally priced at $50. What is the sale price?
First, calculate the discount amount: 0.15 * $50 = $7.50
Then, subtract the discount from the original price: $50 - $7.50 = $42.50
The sale price is $42.50.
Example 2: If the price of a product increased by 20% to reach $60, what was the original price?
Let the original price be 'x'. The equation becomes:
x + 0.20x = $60
1.20x = $60
x = $60 / 1.20
x = $50
The original price was $50.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill applicable across various fields. By understanding the fundamental concepts and applying the methods outlined in this article, you can confidently tackle any percentage problem, from simple calculations to more complex scenarios. Remember to break down the problem, choose the appropriate method, and double-check your work to avoid errors. Practice regularly, and you'll soon find that percentage calculations become second nature. The ability to solve percentage problems efficiently will not only enhance your mathematical skills but also prove invaluable in numerous real-world situations.
Latest Posts
Latest Posts
-
Is Explode A Physical Or Chemical Change
May 10, 2025
-
How To Find Two Tailed P Value
May 10, 2025
-
Is 40 A Prime Or Composite Number
May 10, 2025
-
A Solution With A Ph Of 8 6 Would Be
May 10, 2025
-
Calculate The Ph Of A 0 155 M Solution Of Koh
May 10, 2025
Related Post
Thank you for visiting our website which covers about 25 Of What Number Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.