23 Is What Percent Of 100
listenit
May 24, 2025 · 5 min read
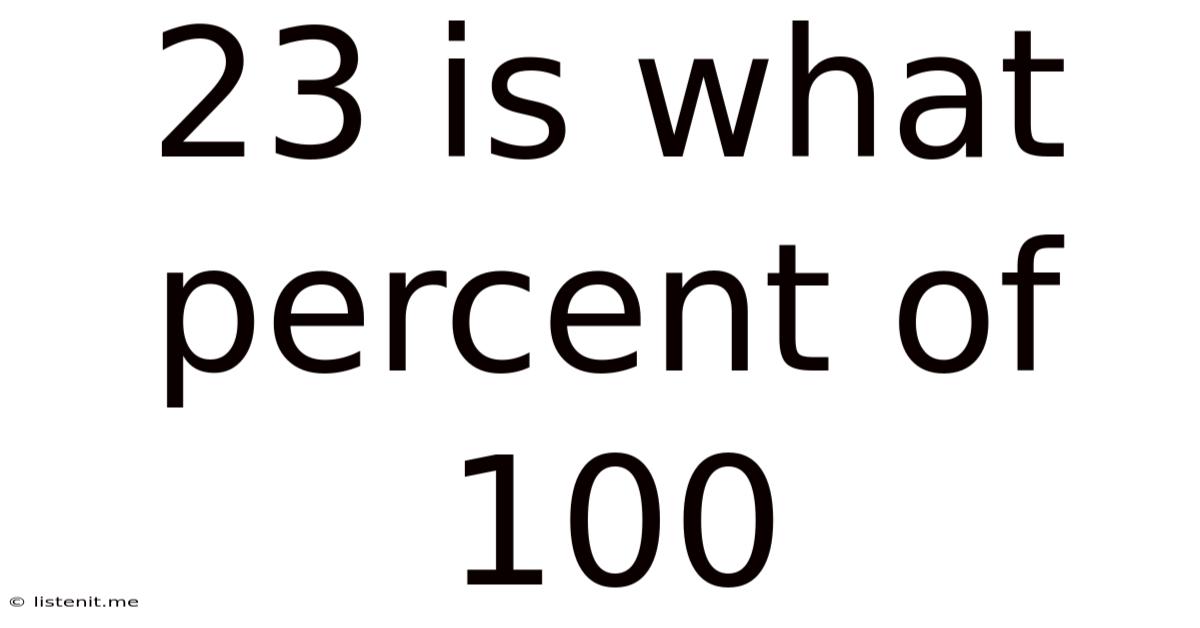
Table of Contents
23 is What Percent of 100? A Comprehensive Guide to Percentages
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve percentage problems, such as "23 is what percent of 100?", is crucial for navigating these scenarios effectively. This comprehensive guide will delve into the solution, exploring different approaches, practical applications, and related concepts to build a solid understanding of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per cent" is Latin for "out of a hundred"). Therefore, 23% means 23 out of 100, or 23/100. This representation allows for easy comparison and understanding of proportions.
Solving "23 is What Percent of 100?"
The question "23 is what percent of 100?" can be solved using several methods:
Method 1: Direct Calculation
This is the most straightforward method. Since a percentage is a fraction of 100, we can directly express the relationship as a fraction and then convert it to a percentage:
- Set up the fraction: 23/100
- Convert to a percentage: 23/100 * 100% = 23%
Therefore, 23 is 23% of 100.
Method 2: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 23
- Whole: 100
Plugging these values into the formula:
(23 / 100) * 100% = 23%
This confirms that 23 is 23% of 100.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve the problem. We can set up a proportion:
23/100 = x/100
Where 'x' represents the percentage we are trying to find. Solving for x:
x = (23/100) * 100 = 23
Therefore, x = 23%, confirming that 23 is 23% of 100.
Practical Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world scenarios:
1. Financial Calculations:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions. For example, if you deposit $1000 in a savings account with a 5% annual interest rate, you will earn $50 in interest after one year.
- Discounts and sales: Stores use percentages to advertise discounts and sales. Knowing how to calculate percentages allows you to determine the actual price after a discount. For instance, a 20% discount on a $50 item means you will pay $40.
- Taxes: Taxes are often calculated as a percentage of income or the value of goods and services. Understanding tax percentages helps in budgeting and financial planning.
- Investment returns: Investors use percentages to track the performance of their investments. A positive percentage indicates a gain, while a negative percentage shows a loss.
2. Academic Performance:
- Grades: Grades are often expressed as percentages reflecting the proportion of correct answers or the overall performance in a test or course. A score of 85% indicates that you answered 85 out of 100 questions correctly.
- Statistical analysis: Percentages are used extensively in statistical analysis to represent proportions and trends within data sets.
3. Daily Life:
- Shopping: Calculating discounts and sales taxes while shopping involves the use of percentages.
- Tipping: Restaurant tips are often calculated as a percentage of the total bill.
- Surveys and polls: Results of surveys and polls are often presented in percentages to show the proportion of respondents who chose a specific option.
Expanding the Concept: Beyond "23 is What Percent of 100?"
While the example "23 is what percent of 100?" provides a clear and simple illustration, the principle of percentage calculation can be applied to any two numbers. Let's consider a more general example:
"X is what percent of Y?"
To solve this, we utilize the same percentage formula:
(X / Y) * 100% = Percentage
Where:
- X represents the part.
- Y represents the whole.
For instance, if we want to determine what percent 15 is of 50:
(15 / 50) * 100% = 30%
Thus, 15 is 30% of 50.
Advanced Percentage Problems and Applications
Beyond basic calculations, percentage problems can become more complex, incorporating multiple steps or requiring a deeper understanding of mathematical concepts. Some advanced applications include:
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's a crucial concept in finance and investment.
- Percentage change: This measures the relative change between two values. For example, calculating the percentage increase or decrease in sales over time. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100%. - Percentage point difference: This is crucial in understanding changes in percentages themselves. If interest rates increase from 2% to 5%, it's a 3 percentage point increase, not a 150% increase.
- Weighted averages: These are averages where different data points contribute differently to the overall average, often weighted by percentages.
Mastering Percentages: Tips and Practice
Becoming proficient in percentage calculations requires consistent practice. Here are some helpful tips:
- Understand the concepts: Ensure you have a solid grasp of fractions, decimals, and ratios, as they are fundamental to understanding percentages.
- Practice regularly: Work through various percentage problems of increasing difficulty. Start with simple examples and gradually progress to more complex scenarios.
- Use different methods: Familiarize yourself with multiple methods for calculating percentages, such as the direct calculation, the formula method, and the proportion method. This will help you choose the most efficient approach for a given problem.
- Utilize online resources: Many websites and apps provide interactive exercises and quizzes to help you practice percentage calculations.
- Check your work: Always double-check your calculations to ensure accuracy. Use a calculator when necessary to avoid errors in manual calculations.
Conclusion
Understanding how to calculate percentages, as exemplified by the question "23 is what percent of 100?", is a valuable skill applicable across numerous disciplines and daily situations. Mastering this fundamental skill empowers you to make informed decisions, analyze data effectively, and navigate various aspects of life with greater confidence and accuracy. From financial planning to academic performance, percentages provide a crucial framework for understanding proportions and making sense of quantitative data. By practicing regularly and exploring different methods, you can build a strong foundation in percentage calculations and apply them effectively in various contexts.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 3 And 9
May 24, 2025
-
What Is 4 2 As A Fraction
May 24, 2025
-
What Is 30 Percent Of 40 Dollars
May 24, 2025
-
Common Factors Of 14 And 35
May 24, 2025
-
X 2 4 X 2 4
May 24, 2025
Related Post
Thank you for visiting our website which covers about 23 Is What Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.