21 Out Of 35 As A Percentage
listenit
May 24, 2025 · 5 min read
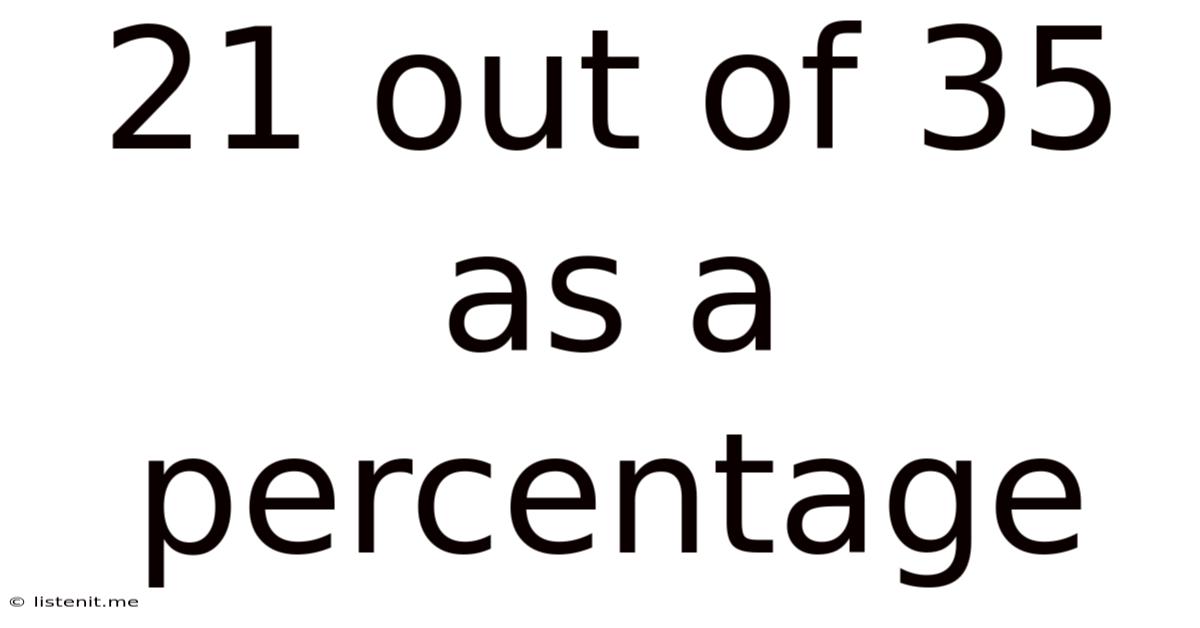
Table of Contents
21 out of 35 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields. Understanding how to calculate percentages allows us to easily compare proportions, analyze data, and make informed decisions in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will delve into the specifics of converting the fraction 21 out of 35 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts.
Understanding Percentages
Before we dive into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5.
The ability to convert fractions to percentages is crucial for various reasons:
- Data Interpretation: Percentages allow for easy comparison of different proportions, even if they are based on different total amounts. For example, comparing a company's profit margin as a percentage across different financial years is more meaningful than comparing raw profit figures.
- Financial Calculations: From calculating interest rates to understanding discounts, sales tax, and tips, percentages are fundamental in financial literacy.
- Statistical Analysis: Percentages are widely used in statistical analyses to represent proportions within datasets, making it easier to interpret results and draw conclusions.
- Everyday Life: From calculating discounts in shopping to understanding survey results, percentages are integral to making sense of everyday numerical data.
Method 1: Using the Formula
The most straightforward way to calculate the percentage is to use the following formula:
(Part / Whole) * 100% = Percentage
In our case, the "part" is 21 and the "whole" is 35. Substituting these values into the formula, we get:
(21 / 35) * 100% = ?
First, we simplify the fraction:
21/35 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 7. This gives us:
21 ÷ 7 = 3 35 ÷ 7 = 5
So, our simplified fraction is 3/5.
Now, we multiply the simplified fraction by 100%:
(3/5) * 100% = 60%
Therefore, 21 out of 35 is 60%.
Method 2: Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100%.
- Convert the fraction to a decimal: Divide the numerator (21) by the denominator (35):
21 ÷ 35 = 0.6
- Multiply by 100%:
0.6 * 100% = 60%
This method confirms our earlier result: 21 out of 35 is indeed 60%.
Method 3: Proportion Method
This method uses the concept of proportions to find the equivalent percentage. We set up a proportion where x represents the percentage we want to find:
21/35 = x/100
To solve for x, we cross-multiply:
35x = 2100
Now, divide both sides by 35:
x = 2100 ÷ 35 = 60
Therefore, x = 60%, confirming our previous calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications across various fields:
1. Business and Finance:
- Profit margins: Businesses use percentages to calculate their profit margins, comparing profits to the cost of goods sold.
- Sales tax: Calculating sales tax on purchases requires understanding percentage calculations.
- Discounts and markdowns: Determining discounts offered during sales involves calculating percentages.
- Investment returns: Investors track their investment returns as percentages to measure performance.
- Interest rates: Calculating interest on loans or savings accounts relies heavily on percentage calculations.
2. Everyday Life:
- Tip calculations: Calculating tips in restaurants often involves determining a percentage of the bill.
- Shopping discounts: Finding the final price after a percentage discount is a common application.
- Survey results: Understanding survey results often involves interpreting data presented as percentages.
- Grade calculations: Many educational systems use percentages to represent grades and academic performance.
- Recipe scaling: Adjusting recipe quantities based on the number of servings involves percentage calculations.
3. Science and Statistics:
- Data analysis: Scientists use percentages to represent proportions within data sets and draw inferences.
- Probability calculations: Percentages are used to express probabilities of events occurring.
- Experimental results: Researchers present experimental results as percentages to highlight significant findings.
Beyond the Basics: Advanced Percentage Calculations
While converting 21 out of 35 to a percentage is relatively straightforward, more complex scenarios can arise. Here are some examples:
- Calculating percentage increase or decrease: This involves comparing two values and determining the percentage change. For example, if a product's price increased from $50 to $60, the percentage increase would be calculated as ((60-50)/50) * 100% = 20%.
- Finding the original value after a percentage change: This often involves working backwards from a final value to determine the original value before a percentage increase or decrease.
- Solving percentage word problems: Word problems requiring the application of percentage concepts can often involve multiple steps and require careful analysis to determine the correct calculation.
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The key to mastering percentage calculations is consistent practice. Try solving various percentage problems to build your understanding.
- Understand the underlying concepts: Focus on grasping the fundamental concept of percentages as parts of 100.
- Use different methods: Familiarize yourself with different methods of calculating percentages to find the approach that best suits your understanding.
- Check your work: Always double-check your calculations to avoid errors.
- Utilize online resources: Many online resources, including calculators and tutorials, can help you practice and improve your skills.
Conclusion
Converting 21 out of 35 to a percentage, resulting in 60%, is a fundamental skill with far-reaching applications. By understanding the various methods and exploring real-world examples, you can develop a strong grasp of percentage calculations and confidently apply them to various situations in your personal and professional life. Remember that practice and a solid understanding of the underlying concepts are key to mastering this essential mathematical skill. Continuous practice and exploration of different calculation methods will solidify your understanding and enable you to confidently tackle more complex percentage problems. Through understanding and applying these techniques, you’ll find yourself more equipped to handle numerical challenges in various aspects of life.
Latest Posts
Latest Posts
-
One Gallon Gas How Many Miles
May 24, 2025
-
Greatest Common Factor Of 40 And 20
May 24, 2025
-
What Is The Highest Common Factor Of 14 And 18
May 24, 2025
-
Least Common Multiple Of 24 And 80
May 24, 2025
-
What Is The Greatest Common Factor Of 24 And 56
May 24, 2025
Related Post
Thank you for visiting our website which covers about 21 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.