What Is The Greatest Common Factor Of 24 And 56
listenit
May 24, 2025 · 5 min read
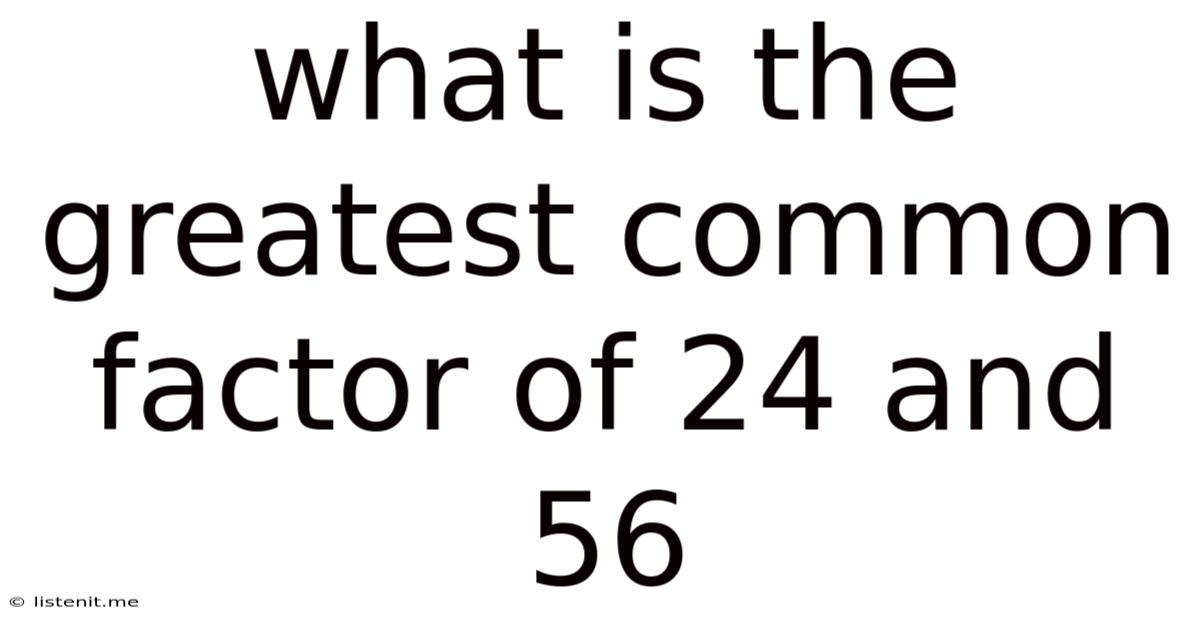
Table of Contents
What is the Greatest Common Factor of 24 and 56? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens doors to a deeper appreciation of number theory and its applications in various fields. This article will explore the GCF of 24 and 56 comprehensively, not just providing the answer but also delving into various methods, practical applications, and the broader mathematical significance of GCF.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding this definition is crucial before we tackle the specific problem of finding the GCF of 24 and 56.
Why is GCF Important?
The GCF is a fundamental concept in mathematics with applications in various fields:
-
Simplification of Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, if we have the fraction 24/56, finding the GCF helps reduce it to its simplest form.
-
Algebraic Simplification: GCF plays a crucial role in simplifying algebraic expressions by factoring out common terms.
-
Problem Solving: Many real-world problems, from dividing items into equal groups to determining the size of the largest square tile that can cover a rectangular area, involve finding the GCF.
-
Cryptography: Number theory, including concepts like GCF, forms the basis of many modern cryptographic systems.
Methods for Finding the GCF of 24 and 56
Several methods exist to determine the GCF of two numbers. Let's explore some of the most common ones:
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
Comparing the two lists, we can see that the common factors are 1, 2, 4, and 8. The greatest common factor is 8.
This method is straightforward for smaller numbers, but it becomes cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method uses the prime factorization of each number to find the GCF. Prime factorization involves expressing a number as a product of its prime factors.
Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3 Prime factorization of 56: 2 x 2 x 2 x 7 = 2³ x 7
The common prime factors are 2³, which is 2 x 2 x 2 = 8. Therefore, the GCF of 24 and 56 is 8.
This method is more efficient than the listing factors method, especially for larger numbers. It provides a more structured approach to finding the GCF.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 24 and 56:
- 56 - 24 = 32 (Now we find the GCF of 24 and 32)
- 32 - 24 = 8 (Now we find the GCF of 24 and 8)
- 24 - 8 = 16 (Now we find the GCF of 16 and 8)
- 16 - 8 = 8 (Now we find the GCF of 8 and 8)
Since both numbers are now 8, the GCF of 24 and 56 is 8.
The Euclidean algorithm is efficient because it reduces the size of the numbers at each step, leading to a faster solution.
Applications of GCF in Real-World Scenarios
The concept of GCF extends far beyond the realm of theoretical mathematics. Let's explore some practical applications:
-
Dividing Items into Groups: Imagine you have 24 apples and 56 oranges. You want to divide them into equal groups, with each group containing the same number of apples and oranges. The GCF (8) tells you that you can create 8 groups, each with 3 apples and 7 oranges.
-
Gardening: Suppose you want to create a rectangular garden with dimensions that are whole numbers. You have 24 feet of fencing for one side and 56 feet for the other. The largest square tile you can use without cutting any tiles is determined by the GCF of 24 and 56, which is 8 feet.
-
Music: Musical harmonies and rhythms often involve finding common factors. Understanding GCF can help in creating consistent and pleasing musical patterns.
-
Computer Programming: The GCF is used in various algorithms related to number theory and cryptography.
-
Engineering: GCF is applied in areas like gear ratios and mechanical design, where finding common divisors is crucial for efficient operation.
Beyond the GCF of 24 and 56: Exploring Further
While this article has focused on finding the GCF of 24 and 56, the underlying principles can be extended to any pair of integers, or even multiple integers. The methods discussed – listing factors, prime factorization, and the Euclidean algorithm – are all valuable tools in number theory and have broader applications in mathematics and beyond.
Understanding the GCF is essential for mastering many mathematical concepts. Its applications in everyday life and various fields highlight its practical significance. The seemingly simple question of finding the GCF of 24 and 56 opens a door to a deeper appreciation of the elegant world of number theory. By mastering different methods for calculating the GCF, you equip yourself with powerful tools for problem-solving and a deeper understanding of mathematical relationships. This knowledge empowers you to tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts. The seemingly simple arithmetic operation holds a surprising depth, revealing the beauty and utility of fundamental mathematical principles.
Latest Posts
Latest Posts
-
Calculate Property Value Based On Rental Income
May 24, 2025
-
What Is 9 In A Fraction
May 24, 2025
-
How Much Wood Chips Do I Need
May 24, 2025
-
What Is 4 4 As A Fraction
May 24, 2025
-
How Many Days Is In Two Months
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 24 And 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.