2/5 As A Decimal And Percentage
listenit
Mar 27, 2025 · 5 min read
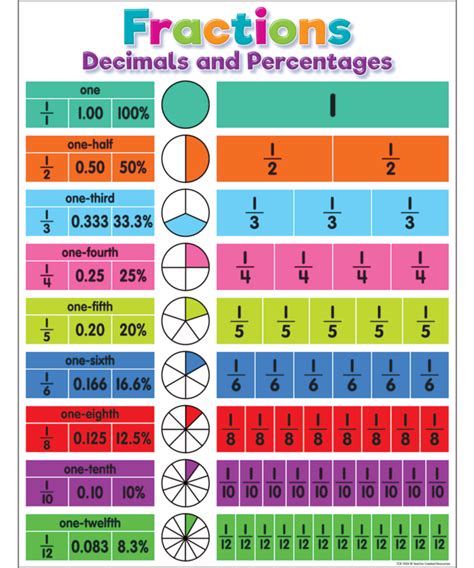
Table of Contents
2/5 as a Decimal and Percentage: A Comprehensive Guide
Understanding fractions, decimals, and percentages is fundamental to various aspects of life, from everyday budgeting to complex scientific calculations. This comprehensive guide delves into the conversion of the fraction 2/5 into its decimal and percentage equivalents, exploring the underlying mathematical principles and providing practical examples to solidify your understanding. We'll also cover related concepts and provide tips for tackling similar conversions.
Understanding Fractions, Decimals, and Percentages
Before we dive into the conversion of 2/5, let's refresh our understanding of these three representations of numerical values:
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
Decimals: Decimals represent a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part. For instance, 0.5 represents 5/10, and 0.25 represents 25/100.
Percentages: Percentages represent a fraction where the denominator is always 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 50% means 50/100, which simplifies to 1/2.
Converting 2/5 to a Decimal
To convert a fraction to a decimal, you simply divide the numerator by the denominator. In this case:
2 ÷ 5 = 0.4
Therefore, 2/5 as a decimal is 0.4.
This process can be easily performed using a calculator or by performing long division manually. Long division provides a deeper understanding of the conversion process, particularly helpful for more complex fractions. Let's illustrate the long division method:
0.4
5 | 2.0
-2.0
0
We add a decimal point and a zero to the 2, allowing us to divide 20 by 5. The result is 4, giving us the decimal 0.4.
Converting 2/5 to a Percentage
There are two main ways to convert a fraction to a percentage:
Method 1: Convert to a decimal, then multiply by 100
This is the most straightforward method. We already know that 2/5 as a decimal is 0.4. To convert this decimal to a percentage, we simply multiply it by 100:
0.4 x 100 = 40
Therefore, 2/5 as a percentage is 40%.
Method 2: Convert the fraction to an equivalent fraction with a denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. We can achieve this by finding a number that, when multiplied by the denominator (5), results in 100. In this case, that number is 20 (5 x 20 = 100). We must then multiply both the numerator and the denominator by 20 to maintain the fraction's value:
(2 x 20) / (5 x 20) = 40/100
Since a percentage is a fraction with a denominator of 100, 40/100 is equivalent to 40%.
Practical Applications of 2/5, 0.4, and 40%
Understanding the interchangeability of these three representations is crucial in various real-world scenarios:
- Calculating discounts: A 40% discount on a $100 item means a reduction of $40 (0.4 x $100 = $40).
- Determining proportions: If 2 out of 5 apples are red (2/5), this represents 40% of the apples being red.
- Understanding data: In statistical analysis, data is often represented as percentages or decimals, making it essential to understand their fractional equivalents.
- Financial calculations: Interest rates, loan repayments, and investment returns frequently use percentages and decimals.
Converting Other Fractions to Decimals and Percentages
The methods outlined above can be applied to convert any fraction to a decimal and a percentage. Here are a few examples:
- 1/4: 1 ÷ 4 = 0.25 = 25%
- 3/8: 3 ÷ 8 = 0.375 = 37.5%
- 7/10: 7 ÷ 10 = 0.7 = 70%
Remember, the key steps are:
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Percentage: Multiply the decimal by 100.
- Fraction to Percentage: Either convert to a decimal first and then to a percentage, or find an equivalent fraction with a denominator of 100.
Dealing with Recurring Decimals
Some fractions, when converted to decimals, result in recurring decimals (decimals that repeat infinitely). For example, 1/3 = 0.3333... In such cases, you can either round the decimal to a certain number of decimal places or represent it using a bar notation (e.g., 0.3̅).
Advanced Concepts and Further Exploration
For more advanced understanding, explore concepts like:
- Rational and Irrational Numbers: Fractions represent rational numbers (numbers that can be expressed as a fraction of two integers). Decimals that don't repeat or terminate represent irrational numbers.
- Significant Figures and Rounding: Understanding significant figures is crucial when working with decimals, especially when dealing with measurements and scientific data.
Conclusion
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill with wide-ranging applications. The conversion of 2/5 to its decimal (0.4) and percentage (40%) equivalent demonstrates the simple yet powerful methods used in this transformation. By mastering these conversions, you'll be better equipped to tackle various mathematical problems and real-world challenges. Practice regularly with different fractions to solidify your understanding and build confidence in handling numerical representations effectively. Remember, consistent practice is key to mastering these essential mathematical concepts.
Latest Posts
Latest Posts
-
Unit Weight Of Water In Lb Ft3
Mar 30, 2025
-
What Are The Common Factors Of 4 And 6
Mar 30, 2025
-
What Is The Gcf Of 64 And 32
Mar 30, 2025
-
Write The Condensed Structure For The Molecule Shown
Mar 30, 2025
-
How To Get From Vertex Form To Factored Form
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about 2/5 As A Decimal And Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
