2 3 Divided By 4 5
listenit
May 23, 2025 · 5 min read
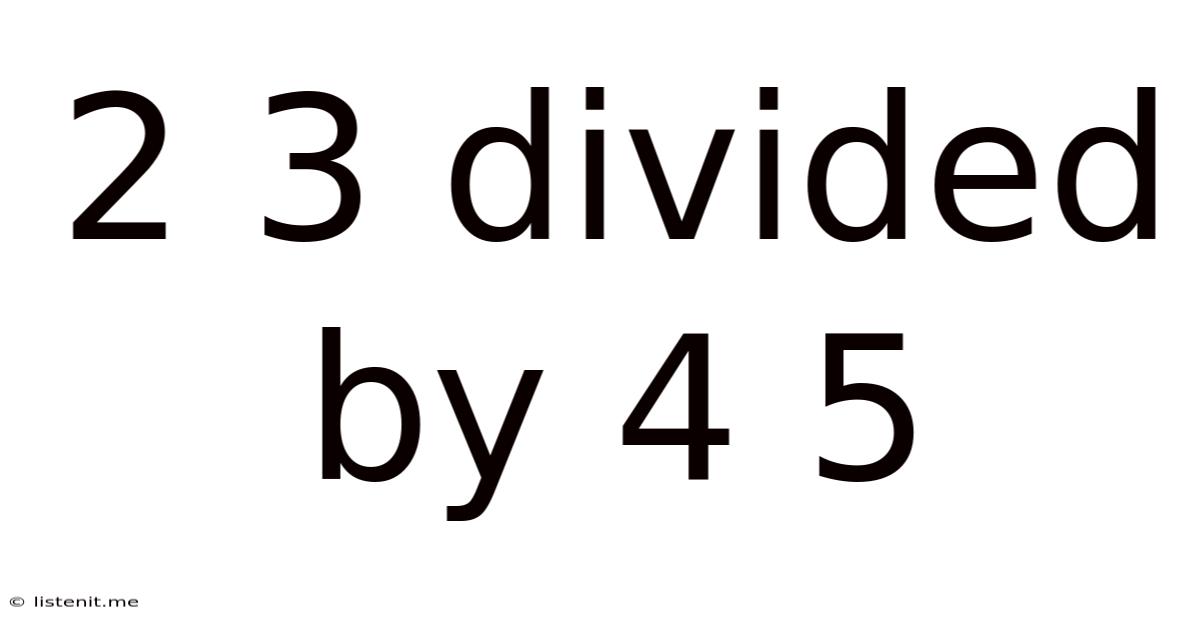
Table of Contents
Decoding the Enigma: A Deep Dive into 23 ÷ 45
The seemingly simple mathematical expression "23 divided by 45" might appear straightforward at first glance. However, a deeper exploration reveals a fascinating interplay of mathematical concepts, practical applications, and even unexpected connections to other fields. This article delves into the intricacies of this division problem, exploring its various facets and demonstrating its relevance beyond a basic arithmetic exercise.
Understanding the Fundamentals: Division as a Process
Before delving into the specifics of 23 ÷ 45, let's establish a foundational understanding of division itself. Division, in its essence, is the process of splitting a quantity into equal parts. It's the inverse operation of multiplication, meaning that if we multiply the quotient (the result of division) by the divisor (the number we're dividing by), we should obtain the dividend (the number being divided).
In our case, the dividend is 23, and the divisor is 45. This implies that we're trying to determine how many times 45 goes into 23, or equivalently, what fraction of 45 represents 23.
The Nature of the Result: Decimals and Fractions
Since 23 is smaller than 45, the result of the division will be less than 1. We can express this result in two primary ways: as a decimal or as a fraction.
-
Decimal Representation: Performing the division yields a decimal value. Calculating 23 ÷ 45 using a calculator or long division gives us approximately 0.5111.... The "..." indicates that the decimal continues infinitely, with the digit 1 repeating. This is a recurring decimal.
-
Fractional Representation: The fractional representation offers a more precise and concise way to depict the result. The fraction representing 23 divided by 45 is simply 23/45. This fraction is already in its simplest form, meaning there's no common factor (other than 1) that can divide both the numerator (23) and the denominator (45). This is an important aspect of mathematical representation: using the simplest possible form to avoid unnecessary complexity.
Exploring the Context: Practical Applications
While 23 ÷ 45 might seem like an abstract mathematical exercise, its underlying principles find practical application across diverse fields. Let's consider a few examples:
Proportions and Ratios
The concept of division forms the bedrock of understanding proportions and ratios. Imagine a scenario involving mixing ingredients. If a recipe calls for 45 units of ingredient A and 23 units of ingredient B, the ratio of ingredient B to ingredient A would be 23:45. The decimal or fractional representation of 23 ÷ 45 (approximately 0.5111 or 23/45) expresses the proportion of ingredient B relative to ingredient A. This understanding is crucial in fields like cooking, chemistry, and engineering where precise proportions are essential.
Percentage Calculations
Percentages are fundamentally about fractions expressed relative to 100. To determine what percentage 23 is of 45, we can simply multiply the decimal result of 23 ÷ 45 by 100. This gives us approximately 51.11%. This calculation is ubiquitous in various contexts: calculating grades, analyzing market share, or determining discount percentages.
Probability and Statistics
In probability and statistics, division plays a critical role in calculating probabilities and frequencies. If 23 out of 45 events resulted in a specific outcome, the probability of that outcome is 23/45, or approximately 0.5111. This understanding underpins statistical analysis and inference in many fields, including research, data science, and risk assessment.
Delving Deeper: Mathematical Properties and Relationships
Beyond its practical applications, the expression 23 ÷ 45 offers opportunities to explore deeper mathematical concepts and relationships.
Prime Factorization and Divisibility
Understanding the prime factorization of both 23 and 45 can provide insights into the nature of their divisibility. 23 is a prime number (only divisible by 1 and itself), while 45 factors into 3² x 5. The lack of common prime factors between 23 and 45 reinforces the fact that the fraction 23/45 is already in its simplest form. This analysis highlights the importance of prime factorization in understanding divisibility and simplification of fractions.
Continued Fractions
The recurring decimal representation of 23 ÷ 45 can be expressed as a continued fraction, a fascinating way to represent rational numbers (fractions) as an infinite series of fractions. While deriving the continued fraction for 23/45 requires a specific algorithm, it demonstrates an alternate and potentially insightful way of representing this seemingly simple division. Continued fractions have applications in number theory and approximation theory.
Approximations and Error Analysis
In practical applications, we often work with approximations. Rounding 0.5111... to 0.51 or 0.52 introduces an error. Understanding the magnitude of this error is crucial in fields like engineering and scientific calculations where precision is paramount. Error analysis helps determine the acceptable level of approximation based on the context and the implications of the error.
Beyond the Numbers: Connecting to Broader Concepts
The simplicity of the problem "23 divided by 45" belies its potential for exploring broader mathematical and conceptual connections.
The Power of Representation
The problem highlights the power of different representations in mathematics. We can represent the result as a decimal, a fraction, or even a continued fraction, each with its own strengths and weaknesses depending on the context. The choice of representation affects how we understand and utilize the result.
The Importance of Precision
The recurring decimal representation emphasizes the importance of precision in mathematical calculations. While we can approximate the value, the underlying mathematical truth is a recurring decimal, highlighting the limits of decimal representation for certain numbers.
Mathematical Curiosity and Exploration
The seemingly simple problem "23 divided by 45" serves as a springboard for exploration. It encourages curiosity about deeper mathematical concepts, such as prime factorization, continued fractions, and error analysis. This curiosity fuels mathematical progress and innovation.
Conclusion: The Unfolding Story of 23 ÷ 45
This deep dive into "23 divided by 45" has unveiled a rich tapestry of mathematical concepts, practical applications, and intellectual explorations. While initially appearing as a simple arithmetic problem, it serves as a microcosm of the elegance and power of mathematics, highlighting the interconnectedness of different mathematical fields and their profound impact on our understanding of the world. It reminds us that even the simplest of mathematical expressions can hold surprising depths and inspire further investigation. The true value lies not just in the answer itself, but in the journey of understanding the processes and concepts it reveals.
Latest Posts
Latest Posts
-
What Is 14 As A Fraction
May 24, 2025
-
What Is The Gcf Of 32 And 40
May 24, 2025
-
6pm To 5am Is How Many Hours
May 24, 2025
-
How Many Days Since April 19
May 24, 2025
-
What Is The Gcf Of 7 And 28
May 24, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.