2 3 Divided By 3 4
listenit
Mar 27, 2025 · 5 min read
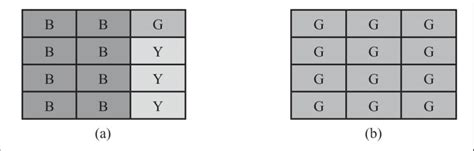
Table of Contents
Decoding the Enigma: A Deep Dive into 2/3 Divided by 3/4
The seemingly simple mathematical expression "2/3 divided by 3/4" often trips up students and even seasoned mathematicians when approached without a clear understanding of the underlying principles. This article aims to demystify this fraction division, providing a comprehensive exploration of the process, its applications, and related concepts. We'll move beyond simply providing the answer, and delve into the why behind the solution, ensuring a thorough understanding that can be applied to a wider range of fraction problems.
Understanding Fraction Division: The Basics
Before we tackle the specific problem of 2/3 divided by 3/4, let's establish a solid foundation in fraction division. The core concept revolves around the idea of finding out "how many times" one fraction fits into another. Unlike whole number division, where we're concerned with how many whole units are contained within another, fraction division deals with fractional parts.
Think of it this way: if you have 2/3 of a pizza, and you want to divide that into portions of 3/4 of a pizza, how many 3/4 portions can you get? This is essentially what the division problem is asking. This visual representation often makes the concept more intuitive.
The "Keep, Change, Flip" Method: A Practical Approach
The most common and arguably the easiest method for dividing fractions is the "Keep, Change, Flip" (or KCF) method. It's a mnemonic device that helps simplify the process:
-
Keep: Keep the first fraction exactly as it is. In our case, this is 2/3.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or invert) the second fraction. This means switching the numerator and the denominator. So, 3/4 becomes 4/3.
Applying this to our problem:
2/3 ÷ 3/4 becomes 2/3 × 4/3
Now, we have a simple multiplication problem.
Multiplying Fractions: A Refresher
Multiplying fractions is straightforward: multiply the numerators together and multiply the denominators together.
(2 × 4) / (3 × 3) = 8/9
Therefore, 2/3 divided by 3/4 equals 8/9.
The Reciprocal Approach: A Deeper Understanding
The "Keep, Change, Flip" method is a shortcut. The underlying mathematical principle is rooted in the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped—switching the numerator and the denominator. Dividing by a fraction is equivalent to multiplying by its reciprocal.
This is why the KCF method works. When we "flip" the second fraction, we're essentially multiplying by its reciprocal.
Visualizing the Solution: A Geometric Approach
While the KCF method provides a quick solution, visualizing the problem can offer a deeper understanding. Imagine a rectangle representing one whole unit. Divide this rectangle into three equal parts horizontally, representing thirds. Shade two of these thirds to represent 2/3. Now, imagine dividing this shaded area into fourths vertically. Counting the resulting shaded squares and comparing them to the total number of squares will visually demonstrate the result of 8/9. This visual approach helps solidify the understanding of fraction division beyond the algebraic manipulation.
Expanding the Concept: More Complex Fraction Division Problems
The principles discussed above apply to more complex fraction division problems. For example, consider the problem:
(5/6) ÷ (2/3) ÷ (1/2)
Here, we'll apply the KCF method step-by-step, working from left to right:
-
(5/6) ÷ (2/3) = (5/6) × (3/2) = 15/12
-
(15/12) ÷ (1/2) = (15/12) × (2/1) = 30/12
Simplifying the final fraction: 30/12 = 5/2 or 2 1/2
Applications of Fraction Division in Real-World Scenarios
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Scaling recipes up or down requires understanding fraction division. If a recipe calls for 2/3 cup of flour, but you want to make half the recipe, you need to divide 2/3 by 2.
-
Construction and Engineering: Calculating measurements and materials often involves fractions. Dividing lengths of wood or other materials to fit specific specifications requires a precise understanding of fraction division.
-
Finance: Dividing shares or portions of investments necessitates calculating fractions.
-
Science: Numerous scientific calculations, particularly in chemistry and physics, involve fraction division for accurate measurements and calculations.
Beyond the Basics: Exploring Mixed Numbers and Improper Fractions
Our initial problem involved proper fractions. However, fraction division can also involve mixed numbers (a whole number and a fraction) and improper fractions (where the numerator is greater than the denominator). To solve these, it's essential to first convert mixed numbers into improper fractions before applying the KCF method.
For example:
1 1/2 ÷ 2/3
First, convert 1 1/2 to an improper fraction: (1 × 2 + 1) / 2 = 3/2
Now apply the KCF method:
3/2 ÷ 2/3 = 3/2 × 3/2 = 9/4 or 2 1/4
Mastering Fraction Division: Tips and Strategies for Success
-
Practice Regularly: The key to mastering fraction division is consistent practice. Work through various problems, starting with simpler ones and gradually increasing the complexity.
-
Visual Aids: Utilize visual aids like diagrams or physical objects to understand the concept better.
-
Break Down Complex Problems: For complex problems, break them down into smaller, manageable steps.
-
Check Your Work: Always check your answer to ensure accuracy.
Conclusion: Embracing the Power of Fractions
Understanding fraction division is a crucial skill with far-reaching applications. While the "Keep, Change, Flip" method provides a convenient shortcut, grasping the underlying principles of reciprocals and the visual representation of fraction division enhances comprehension and allows for solving more complex problems with confidence. By mastering this fundamental concept, you unlock the ability to tackle a wide array of mathematical challenges in various real-world scenarios. So, next time you encounter a fraction division problem, remember the KCF method, visualize the process, and enjoy the journey of unlocking the power of fractions.
Latest Posts
Latest Posts
-
The Mass Of One Mole Of Carbon Dioxide Is
Mar 30, 2025
-
20 Is 85 Of What Number
Mar 30, 2025
-
Protons Neutrons And Electrons Of Bromine
Mar 30, 2025
-
The Half Life Of Carbon 14 Is 5730 Years
Mar 30, 2025
-
In What Units Is Density Measured
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
