18 Is 30 Percent Of What Number
listenit
May 24, 2025 · 4 min read
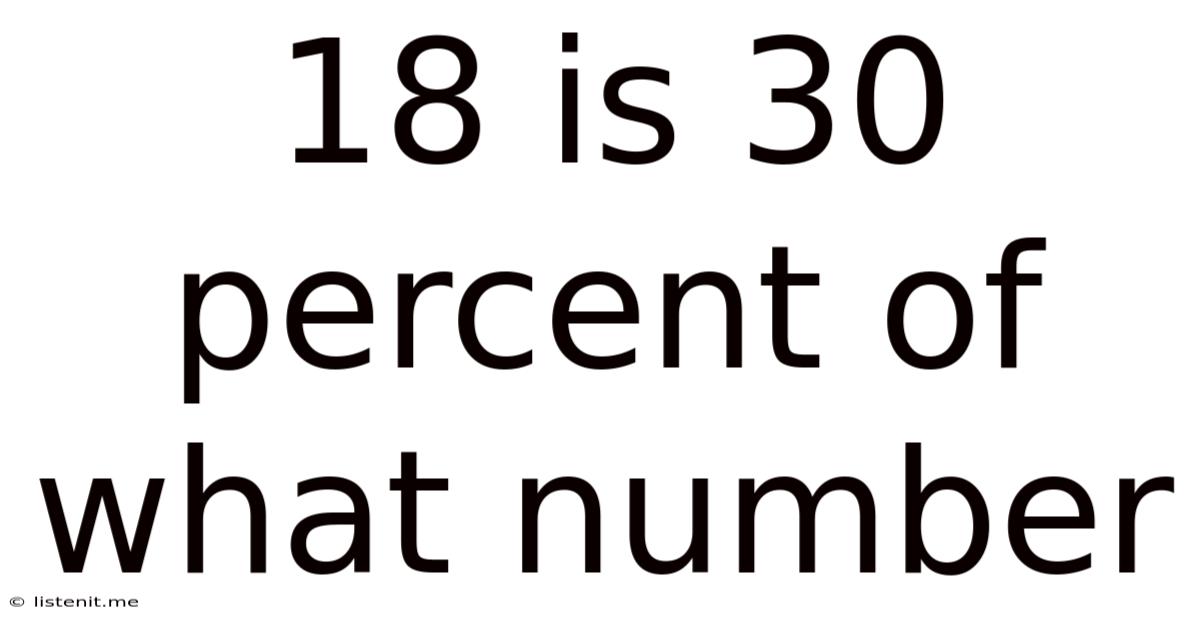
Table of Contents
18 is 30 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article delves deep into the question, "18 is 30 percent of what number?", providing not only the solution but also a comprehensive understanding of the underlying mathematical principles and various methods to solve similar percentage problems. We'll explore different approaches, ranging from simple algebraic equations to the application of percentage formulas, equipping you with the tools to tackle a wide range of percentage calculations with confidence.
Understanding the Problem: Deconstructing the Percentage Equation
The statement "18 is 30 percent of what number?" can be translated into a mathematical equation. Let's break it down:
- "18 is": This translates to "18 =".
- "30 percent": This is expressed as 0.30 (or 30/100).
- "of what number?": This represents the unknown value, which we'll denote as 'x'.
Therefore, the equation becomes: 18 = 0.30x
This seemingly simple equation forms the foundation for solving the problem. We will now explore several methods to determine the value of 'x'.
Method 1: Solving the Equation Algebraically
This is the most straightforward method. To solve for 'x', we need to isolate it on one side of the equation. We can achieve this by dividing both sides of the equation by 0.30:
18 / 0.30 = 0.30x / 0.30
This simplifies to:
x = 60
Therefore, 18 is 30 percent of 60.
Method 2: Using the Percentage Formula
The fundamental percentage formula is:
(Percentage/100) * Whole = Part
In our problem:
- Part: 18
- Percentage: 30
- Whole: x (the unknown value)
Substituting these values into the formula, we get:
(30/100) * x = 18
Simplifying:
0.30x = 18
Now, we solve for 'x' by dividing both sides by 0.30:
x = 18 / 0.30 = 60
Again, we arrive at the solution: x = 60
Method 3: Applying Proportions
Proportions offer another effective approach to solving percentage problems. We can set up a proportion using the relationship between the percentage and the whole number:
30/100 = 18/x
To solve this proportion, we cross-multiply:
30x = 1800
Then, divide both sides by 30:
x = 1800 / 30 = 60
Once again, the solution is x = 60.
Verifying the Solution
It's crucial to verify the solution to ensure accuracy. We can check our answer by calculating 30% of 60:
(30/100) * 60 = 18
Since this confirms our initial statement, we can confidently conclude that 18 is indeed 30 percent of 60.
Expanding the Concept: Solving Similar Percentage Problems
The methods outlined above are not limited to this specific problem. They are applicable to a wide range of percentage calculations. Let's consider some variations:
Example 1: Finding the Percentage
What percentage of 80 is 20?
Using the formula: (Percentage/100) * 80 = 20
Solving for Percentage: Percentage = (20/80) * 100 = 25%
Example 2: Finding the Whole Number
25 is 15% of what number?
Using the formula: (15/100) * x = 25
Solving for x: x = 25 / (15/100) = 166.67 (approximately)
Example 3: Real-world Application: Discount Calculations
A store offers a 20% discount on an item originally priced at $150. What is the discounted price?
First, calculate the discount amount: (20/100) * $150 = $30
Then, subtract the discount from the original price: $150 - $30 = $120
The discounted price is $120.
Advanced Percentage Concepts and Applications
Beyond basic percentage calculations, several advanced concepts further broaden the application of percentages:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's crucial in understanding savings growth and loan repayments.
-
Percentage Change: This measures the relative change between two values, often used to track growth or decline in various metrics (e.g., sales, population).
-
Percentage Points: This represents the absolute difference between two percentages, often used in comparing changes in rates or proportions.
-
Statistical Applications: Percentages play a vital role in statistical analysis, including frequency distributions, probability calculations, and hypothesis testing.
Mastering Percentages: Tips and Resources
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying principles. Here are some tips to enhance your skills:
-
Practice Regularly: Solve a variety of percentage problems to build your proficiency and confidence.
-
Understand the Formulas: Memorize the basic percentage formula and its variations.
-
Use Different Methods: Experiment with different approaches (algebraic, formula, proportions) to find the method you find most intuitive.
-
Verify Your Answers: Always double-check your calculations to ensure accuracy.
-
Utilize Online Resources: Numerous online calculators and tutorials are available to assist with percentage calculations and further your understanding.
Conclusion: The Power of Percentage Calculations
Understanding and applying percentage calculations is a crucial skill applicable in numerous aspects of life, from personal finance to professional settings. This article provided a comprehensive guide to solving percentage problems, emphasizing various methods and real-world applications. By mastering these techniques, you equip yourself with a powerful tool for navigating and interpreting numerical data effectively. Remember that consistent practice and a solid grasp of the underlying principles are key to achieving proficiency in percentage calculations. Continue practicing, and you'll soon find yourself confidently tackling even the most complex percentage problems.
Latest Posts
Latest Posts
-
How Many Groups Of 1 9 Are In 2
May 24, 2025
-
1300 Is 30 Percent Of What Number
May 24, 2025
-
5 8 As A Whole Number
May 24, 2025
-
Area To The Left Of Z
May 24, 2025
-
Greatest Common Factor Of 48 And 20
May 24, 2025
Related Post
Thank you for visiting our website which covers about 18 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.