How Many Groups Of 1/9 Are In 2
listenit
May 24, 2025 · 5 min read
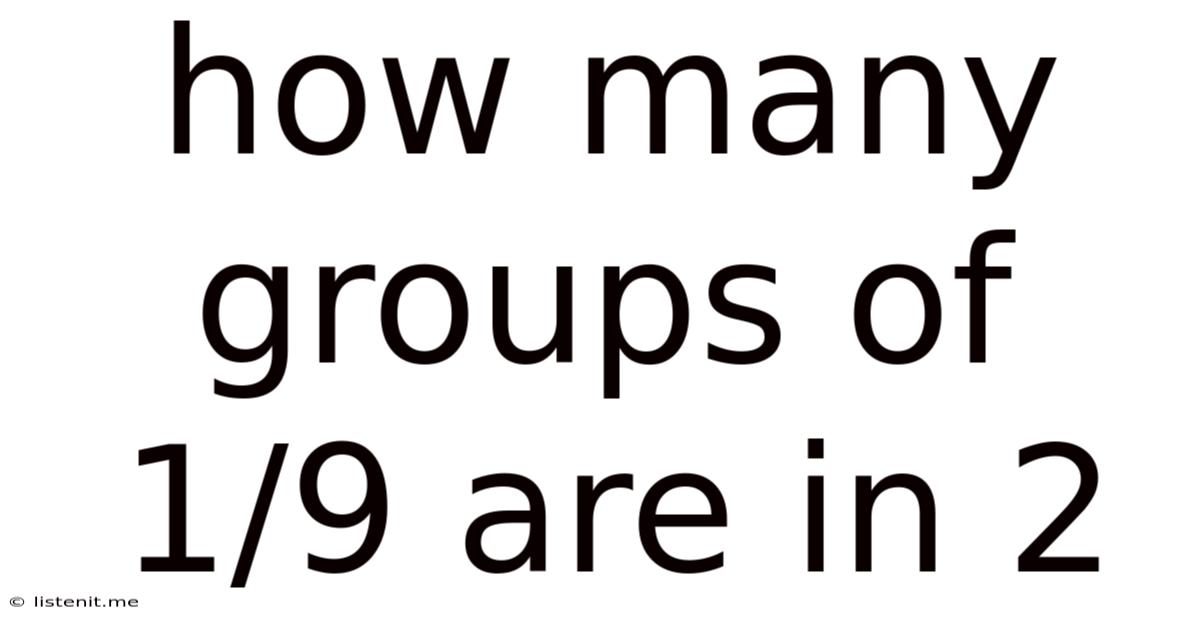
Table of Contents
How Many Groups of 1/9 Are in 2? A Deep Dive into Fraction Division
This seemingly simple question, "How many groups of 1/9 are in 2?", opens the door to a deeper understanding of fraction division, a concept crucial in mathematics and various real-world applications. While the answer might seem immediately obvious to some, exploring the problem through different approaches illuminates the underlying principles and enhances mathematical fluency. This article will dissect this problem, explaining various methods of solving it and highlighting the importance of grasping fraction division.
Understanding the Problem: Visualizing the Concept
Before jumping into the calculations, let's visualize the problem. Imagine you have two whole pizzas. You want to divide each pizza into nine equal slices, representing our 1/9 fraction. The question then becomes: how many of these 1/9 slices do you have in total across both pizzas?
This visual representation immediately gives us an intuitive understanding of the problem. Since each pizza yields nine slices, two pizzas will provide 2 x 9 = 18 slices. Therefore, there are 18 groups of 1/9 in 2.
Method 1: Converting to a Common Denominator
This method involves transforming the whole number (2) into a fraction with the same denominator as the fraction we're dividing by (1/9).
-
Step 1: Express 2 as a fraction. Any whole number can be expressed as a fraction with a denominator of 1. So, 2 becomes 2/1.
-
Step 2: Find a common denominator. The common denominator for 2/1 and 1/9 is 9.
-
Step 3: Convert the fractions. To convert 2/1 to a fraction with a denominator of 9, we multiply both the numerator and denominator by 9: (2/1) x (9/9) = 18/9.
-
Step 4: Divide the fractions. Now, we divide 18/9 by 1/9. Dividing fractions involves multiplying the first fraction by the reciprocal (flipped version) of the second fraction: (18/9) x (9/1) = 18.
Therefore, there are 18 groups of 1/9 in 2.
Method 2: Using the Reciprocal and Multiplication
This method is a more direct approach to fraction division. It leverages the concept that dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Step 1: Find the reciprocal of 1/9. The reciprocal of 1/9 is 9/1 (or simply 9).
-
Step 2: Multiply 2 by the reciprocal. We multiply 2 by 9: 2 x 9 = 18.
Again, this demonstrates that there are 18 groups of 1/9 in 2.
Method 3: Repeated Subtraction
This approach provides a more intuitive understanding of the division process, particularly for those who find the abstract nature of fraction division challenging.
-
Step 1: Start with 2. We begin with our initial value of 2.
-
Step 2: Repeatedly subtract 1/9. We repeatedly subtract 1/9 from 2 until we reach 0.
2 - 1/9 = 1 and 8/9 1 and 8/9 - 1/9 = 1 and 7/9 ...and so on, until we reach 0.
- Step 3: Count the subtractions. The number of times we subtract 1/9 from 2 represents the number of groups of 1/9 in 2. You will find that you subtract 1/9 eighteen times before reaching zero.
This method also confirms that there are 18 groups of 1/9 in 2.
Real-World Applications: Where Fraction Division Matters
Understanding fraction division is not just an academic exercise; it has significant practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require precise measurements, and adjusting recipes requires dividing or multiplying fractions. For instance, if a recipe calls for 1/9 cup of sugar, and you want to make double the recipe, you'll need to calculate 2 x (1/9) cup of sugar.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Dividing lengths or quantities often involves fractions. Imagine dividing a 2-meter plank into sections of 1/9 of a meter; the answer directly uses this type of fraction division.
-
Finance and Budgeting: Dividing budgets, calculating percentages of income, or splitting costs among multiple people often involves working with fractions and decimals, requiring a sound understanding of fraction division.
-
Data Analysis and Statistics: In statistical analysis, interpreting data and calculating probabilities might necessitate dividing fractions, contributing to accurate data interpretation.
-
Sewing and Tailoring: When dealing with fabric measurements, precise calculations involving fractions are essential for accurate cutting and sewing. A tailor working with a 2-meter piece of cloth who needs pieces of 1/9 of a meter will use this exact calculation.
Beyond the Basics: Extending the Concept
The problem "How many groups of 1/9 are in 2?" serves as a foundational example. However, the principles can be extended to more complex problems involving different fractions and whole numbers. The core concepts of finding common denominators, using reciprocals, or repeated subtraction remain relevant regardless of the complexity of the fractions.
Conclusion: Mastering Fraction Division for Success
Mastering fraction division is essential for success in numerous fields and everyday situations. The seemingly simple question of "How many groups of 1/9 are in 2?" provides a valuable opportunity to solidify understanding of this fundamental mathematical operation. By exploring various methods—converting to common denominators, using reciprocals, or repeated subtraction—we gain a comprehensive grasp of the underlying principles, enhancing mathematical problem-solving skills and preparing us for more complex calculations. The ability to confidently handle fractions extends far beyond the classroom, proving incredibly useful in various aspects of life, from cooking and sewing to finance and engineering. The more comfortable you are with this concept, the more equipped you will be to tackle more intricate mathematical challenges and real-world problems that involve fractions.
Latest Posts
Latest Posts
-
What Is The Gcf Of 40 And 63
May 25, 2025
-
How Much Is 20 Off Of 25
May 25, 2025
-
Which Expression Represents The Inverse Of The Matrix Below
May 25, 2025
-
What Is The Percentage Of 14 Out Of 15
May 25, 2025
-
9 1 6 As An Improper Fraction
May 25, 2025
Related Post
Thank you for visiting our website which covers about How Many Groups Of 1/9 Are In 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.