17 Out Of 28 As A Percentage
listenit
May 25, 2025 · 5 min read
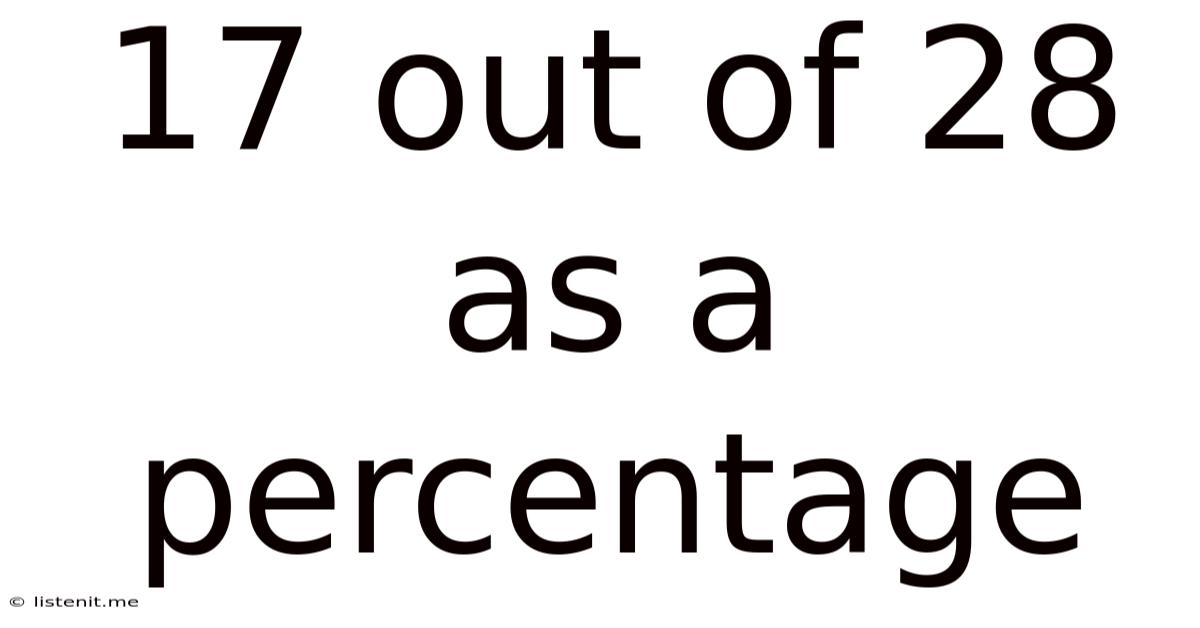
Table of Contents
17 out of 28 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with applications spanning various fields, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and expressing proportions effectively. This article delves into the specific calculation of 17 out of 28 as a percentage, explaining the process step-by-step and exploring related concepts to build a comprehensive understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Percentages are widely used because they provide a standardized way to compare different quantities and proportions.
Calculating 17 out of 28 as a Percentage: The Method
To calculate 17 out of 28 as a percentage, we need to follow these steps:
Step 1: Formulate the Fraction
First, express the given information as a fraction. "17 out of 28" translates to the fraction 17/28.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (17) by the denominator (28):
17 ÷ 28 ≈ 0.6071
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%):
0.6071 × 100 ≈ 60.71%
Therefore, 17 out of 28 is approximately 60.71%.
Rounding Percentages
In many cases, you'll need to round your percentage to a specific number of decimal places. The level of precision required depends on the context. For instance, in informal settings, rounding to the nearest whole number (61%) might suffice. However, for more precise applications, such as scientific research or financial reporting, more decimal places might be necessary. In this case, we've rounded to two decimal places (60.71%).
Practical Applications of Percentage Calculations
Understanding percentage calculations has countless practical applications in everyday life and professional settings. Here are a few examples:
1. Financial Calculations:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Discounts: Stores advertise discounts as percentages (e.g., "20% off"). Calculating the actual price reduction requires understanding percentages.
- Taxes: Taxes are often expressed as percentages of income or the cost of goods and services.
- Investment returns: Investment performance is frequently measured as a percentage return on investment.
2. Academic Performance:
- Grades: Grades are often expressed as percentages, reflecting the proportion of correctly answered questions or the overall performance in a course.
- Test scores: Standardized tests frequently report scores as percentages.
3. Data Analysis:
- Statistical representation: Percentages are essential for summarizing and presenting data in a clear and concise manner. For instance, representing survey results or demographic information.
- Probability: Percentages can express the likelihood of an event occurring.
4. Everyday Life:
- Tipping: Calculating tips in restaurants is often done using percentages.
- Recipe scaling: Adjusting recipe ingredient quantities based on the number of servings involves proportional reasoning and percentages.
- Sales and promotions: Understanding percentage discounts helps make informed purchasing decisions.
Advanced Percentage Calculations: Related Concepts
While calculating 17 out of 28 as a percentage is relatively straightforward, understanding related concepts can enhance your ability to solve more complex problems involving percentages.
1. Finding the Percentage Increase or Decrease:
This involves calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] × 100%
For example, if the price of an item increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] × 100% = 20%
2. Calculating a Percentage of a Number:
To find a percentage of a number, convert the percentage to a decimal and multiply it by the number. For instance, to find 25% of 80:
0.25 × 80 = 20
3. Finding the Original Value After a Percentage Change:
If you know the final value and the percentage change, you can work backward to find the original value. This often requires solving an algebraic equation.
Using Technology for Percentage Calculations
While manual calculations are useful for understanding the underlying principles, technology can significantly simplify and speed up the process, especially for complex problems. Most calculators, spreadsheets (like Microsoft Excel or Google Sheets), and even online tools can easily calculate percentages. These tools can be incredibly helpful when dealing with large datasets or intricate calculations.
Beyond the Numbers: The Importance of Context
It's crucial to remember that percentages are just numbers; they derive meaning from the context in which they're used. A 60.71% success rate on a crucial medical procedure has a vastly different significance than a 60.71% pass rate on a multiple-choice quiz. Always consider the context when interpreting and applying percentage data. A superficial understanding of the percentage alone can lead to misinterpretations and flawed conclusions.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, such as determining 17 out of 28 as a percentage (approximately 60.71%), is a valuable skill with widespread applications. From everyday financial transactions to complex scientific analyses, the ability to accurately calculate and interpret percentages is crucial for making informed decisions and communicating effectively. By mastering the fundamental concepts and exploring related applications, you can significantly enhance your quantitative literacy and problem-solving abilities. Remember to always consider the context and utilize available technological tools to streamline the calculation process. The ability to confidently and accurately work with percentages empowers you to navigate a data-driven world with greater understanding and confidence.
Latest Posts
Latest Posts
-
105k A Year Is How Much A Month
May 25, 2025
-
How Many Calories On Weight Watchers
May 25, 2025
-
What Is 16 Of 43 Minutes
May 25, 2025
-
What Is 8 Out Of 11 As A Percentage
May 25, 2025
-
Calculate Calories Burned By Heart Rate
May 25, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 28 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.