16 Is What Percent Of 200
listenit
May 24, 2025 · 4 min read
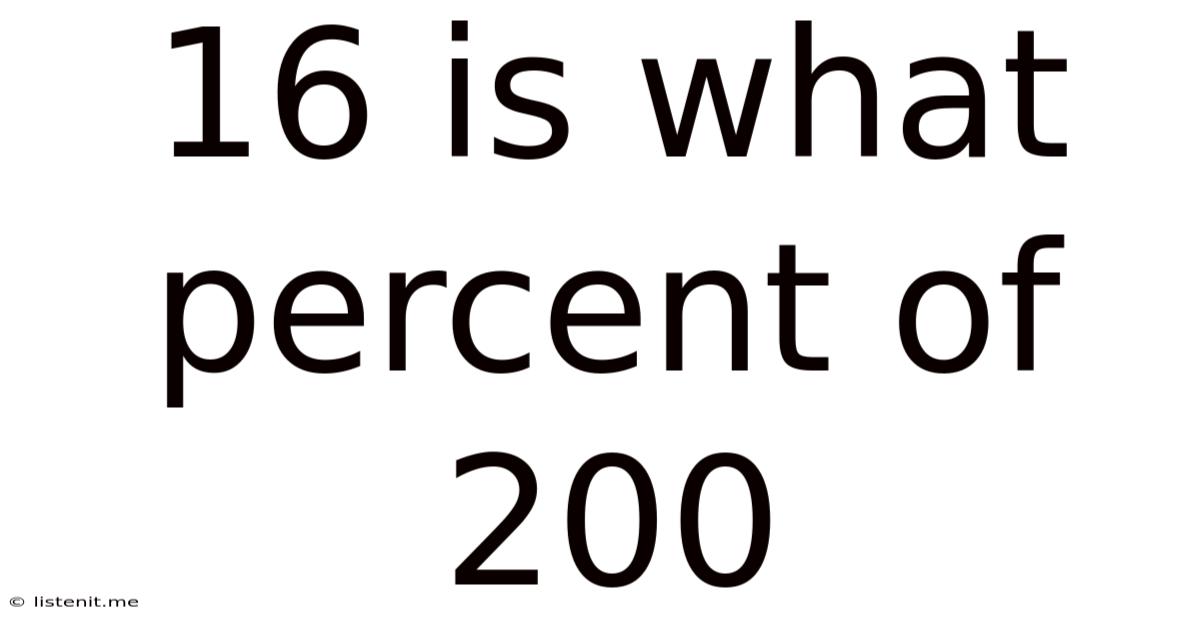
Table of Contents
16 is What Percent of 200? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "16 is what percent of 200?", opens the door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. From calculating discounts in a store to understanding financial reports, percentages are an essential tool. This article will not only answer the question directly but also explore the underlying principles of percentage calculations, offering different approaches and practical examples. We’ll delve into the formula, discuss various methods of solving the problem, and highlight real-world scenarios where this type of calculation proves invaluable.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (per centum in Latin). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating the Percentage: The Formula
The core formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our problem, "16 is what percent of 200?", we identify:
- Part: 16 (the number we're expressing as a percentage)
- Whole: 200 (the total amount)
Applying the formula:
(16 / 200) * 100% = 8%
Therefore, 16 is 8% of 200.
Different Approaches to Solving the Problem
While the formula is straightforward, let's explore alternative methods to solve this problem, reinforcing the understanding of percentages.
Method 1: Using Proportions
We can set up a proportion to solve the problem:
16/200 = x/100
Where 'x' represents the percentage we're trying to find. Cross-multiplying:
16 * 100 = 200 * x
1600 = 200x
x = 1600 / 200
x = 8
Therefore, x = 8%, confirming our earlier result.
Method 2: Decimal Conversion
First, express the fraction 16/200 as a decimal:
16 / 200 = 0.08
Then, convert the decimal to a percentage by multiplying by 100%:
0.08 * 100% = 8%
This method highlights the direct relationship between decimals and percentages.
Method 3: Simplifying the Fraction
Before applying the formula, simplify the fraction 16/200:
16/200 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 16:
16/16 = 1 and 200/16 = 12.5
This simplifies the fraction to 1/12.5. Now apply the formula:
(1 / 12.5) * 100% = 8%
This method demonstrates that simplification can make the calculation easier.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world situations:
-
Sales and Discounts: Stores frequently advertise discounts like "20% off." Calculating the actual savings requires understanding percentages. For example, a 20% discount on a $100 item means a saving of $20 (20% of $100).
-
Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages. Calculating the tax amount on a purchase or income involves percentage calculations.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding interest calculations is essential for managing finances effectively.
-
Financial Statements: Financial reports like balance sheets and income statements use percentages extensively to show ratios and trends. Analyzing these reports requires a strong understanding of percentages.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. For example, expressing survey results or population demographics often involves using percentages.
-
Grade Calculation: In many educational systems, grades are often represented as percentages reflecting the student's performance.
Advanced Percentage Problems and Concepts
Beyond basic percentage calculations, several more advanced concepts build upon this foundation:
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers (e.g., the percentage increase in sales from one year to the next).
-
Compound Interest: Calculating the interest earned on an investment where the interest is added to the principal, and subsequent interest is calculated on the new total.
-
Percentage Points: A crucial distinction – percentage points represent the absolute difference between two percentages, not a relative change. For instance, an increase from 10% to 15% is a 5-percentage-point increase, but a 50% relative increase.
Practice Problems
To solidify your understanding, try these practice problems:
- What is 25% of 80?
- 15 is what percent of 75?
- If a shirt costs $50 and is discounted by 15%, what is the final price?
- A student scored 80 out of 100 on a test. What is their percentage score?
- The price of a house increased from $200,000 to $250,000. What is the percentage increase?
Conclusion
Understanding percentages is a valuable skill with wide-ranging applications. While the basic formula is relatively simple, mastering different approaches and understanding its real-world implications empowers you to tackle various quantitative problems effectively. From managing personal finances to analyzing complex data, the ability to work with percentages is a cornerstone of numerical literacy. This article provides a comprehensive guide, moving from the fundamental formula to more advanced concepts, aiming to equip you with the knowledge to confidently navigate the world of percentage calculations. Remember to practice regularly to build your proficiency and gain a deeper understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
8 Out Of 11 In Percentage
May 24, 2025
-
Furnace Size Calculator By Zip Code
May 24, 2025
-
7 X 10 To The Power Of 4
May 24, 2025
-
What Is 2 To The 20th Power
May 24, 2025
-
Greatest Common Factor Of 3 And 27
May 24, 2025
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.