8 Out Of 11 In Percentage
listenit
May 24, 2025 · 5 min read
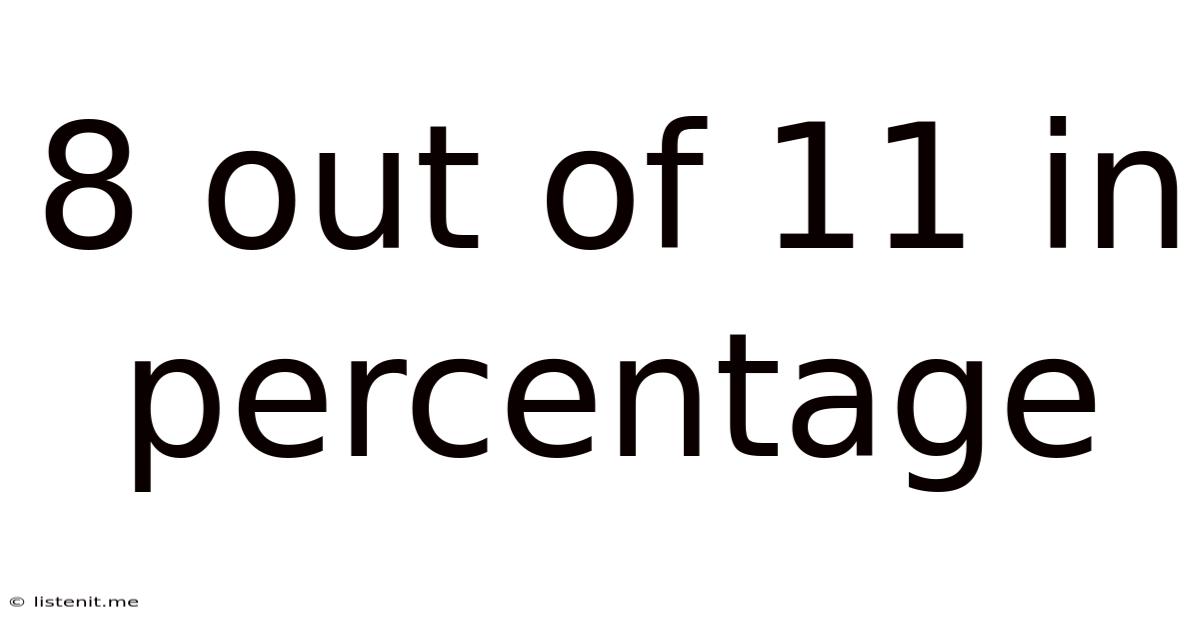
Table of Contents
8 Out of 11: Understanding Percentages and Their Applications
Calculating percentages is a fundamental skill with broad applications across various fields, from everyday budgeting to complex statistical analysis. Understanding how to calculate and interpret percentages allows for clearer communication and more informed decision-making. This article delves deep into the calculation of "8 out of 11" as a percentage, exploring the underlying methods, showcasing practical applications, and examining related percentage calculations.
Calculating 8 Out of 11 as a Percentage
The phrase "8 out of 11" represents a fraction: 8/11. To convert this fraction to a percentage, we follow a simple two-step process:
-
Convert the Fraction to a Decimal: Divide the numerator (8) by the denominator (11). 8 ÷ 11 ≈ 0.7273
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage sign (%). 0.7273 x 100 ≈ 72.73%
Therefore, 8 out of 11 is approximately 72.73%.
Understanding the Concept of Percentages
Percentages provide a standardized way to express proportions or ratios. They represent a fraction of 100, making comparisons and interpretations easier. A percentage is always expressed with a "%" symbol. Understanding percentages involves grasping the relationship between fractions, decimals, and percentages. They are interchangeable and can be converted from one form to another.
Key Concepts:
- Numerator: The top number in a fraction (in this case, 8). It represents the part or portion.
- Denominator: The bottom number in a fraction (in this case, 11). It represents the whole or total.
- Percentage: A number expressed as a fraction of 100.
Practical Applications of Percentage Calculations
The ability to calculate percentages has practical implications across numerous areas of life:
1. Academic Performance:
Imagine a student scoring 8 out of 11 questions correctly on a quiz. Converting this to a percentage (72.73%) provides a clear understanding of their performance relative to the total possible score. This allows for easy comparison with other assessments and helps track academic progress.
2. Business and Finance:
Businesses use percentages extensively:
- Profit margins: Calculating the percentage of profit earned on sales.
- Sales growth: Tracking the percentage increase or decrease in sales over time.
- Discount calculations: Determining the price reduction based on a percentage discount. For example, a 10% discount on a $100 item reduces the price by $10.
- Interest rates: Expressing the cost of borrowing money as a percentage.
- Investment returns: Measuring the percentage increase or decrease in the value of investments.
3. Statistics and Probability:
Percentages are fundamental in statistical analysis. They are used to represent:
- Frequencies: Expressing the occurrence of an event as a percentage of the total number of observations.
- Probabilities: Describing the likelihood of an event occurring as a percentage.
- Confidence intervals: Expressing the range of values within which a population parameter is likely to fall, with a certain degree of confidence.
4. Everyday Life:
Everyday situations where percentage calculations are useful include:
- Tipping in restaurants: Calculating a tip percentage (e.g., 15% or 20%) on the total bill.
- Sales tax: Determining the amount of sales tax added to a purchase price.
- Nutritional information: Understanding the percentage of daily recommended values for nutrients in food.
- Surveys and polls: Interpreting the results of surveys and polls, which are often presented as percentages.
Variations and Related Percentage Calculations
While "8 out of 11" is a straightforward percentage calculation, understanding related concepts enhances your skills:
1. Calculating Percentage Increase or Decrease:
Suppose the initial value is 11 and the final value is 8. To calculate the percentage decrease:
- Find the difference: 11 - 8 = 3
- Divide the difference by the initial value: 3 ÷ 11 ≈ 0.2727
- Multiply by 100 and add the percentage sign: 0.2727 x 100 ≈ 27.27%
Therefore, there is approximately a 27.27% decrease from 11 to 8.
2. Calculating "x" out of "y":
The general formula for calculating "x" out of "y" as a percentage is:
(x/y) * 100%
This formula can be applied to any situation where you need to calculate a percentage based on a part and a whole.
3. Working Backwards from a Percentage:
If you know the percentage and the whole, you can calculate the part. For example, if 72.73% of a number is 8, what is the number?
- Convert the percentage to a decimal: 72.73% = 0.7273
- Divide the part by the decimal: 8 ÷ 0.7273 ≈ 11
This confirms that 8 is indeed 72.73% of 11.
Advanced Applications and Further Learning
Beyond the basic calculations, percentages are utilized in more complex scenarios:
- Compound interest: Interest earned on both the principal and accumulated interest.
- Statistical hypothesis testing: Determining the statistical significance of results.
- Financial modeling: Creating models to predict future financial performance.
- Data analysis and visualization: Representing data using charts and graphs that incorporate percentages.
Mastering percentage calculations opens doors to deeper understanding in various quantitative fields. Further exploration of these advanced applications will strengthen your analytical abilities and enhance your understanding of the world around you.
Conclusion
Understanding how to calculate and interpret percentages is a valuable skill with widespread applications. The simple calculation of 8 out of 11 as approximately 72.73% demonstrates the basic process. However, the ability to apply this knowledge to diverse situations, from assessing academic performance to understanding financial data, highlights the practical significance of this fundamental concept. By mastering the principles of percentage calculations and exploring their varied applications, you equip yourself with essential tools for making informed decisions and engaging with the numerical world more effectively. Remember to practice regularly to solidify your understanding and to confidently tackle various percentage-related problems.
Latest Posts
Latest Posts
-
What Is 30 Percent Of 550
May 25, 2025
-
What Is 1 3 Of 350
May 25, 2025
-
01 To The Power Of 30
May 25, 2025
-
What Is 1 4 Divided By 1 2
May 25, 2025
-
Least Common Multiple Of 5 6 7
May 25, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 11 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.