15 Out Of 40 As A Percentage
listenit
May 25, 2025 · 5 min read
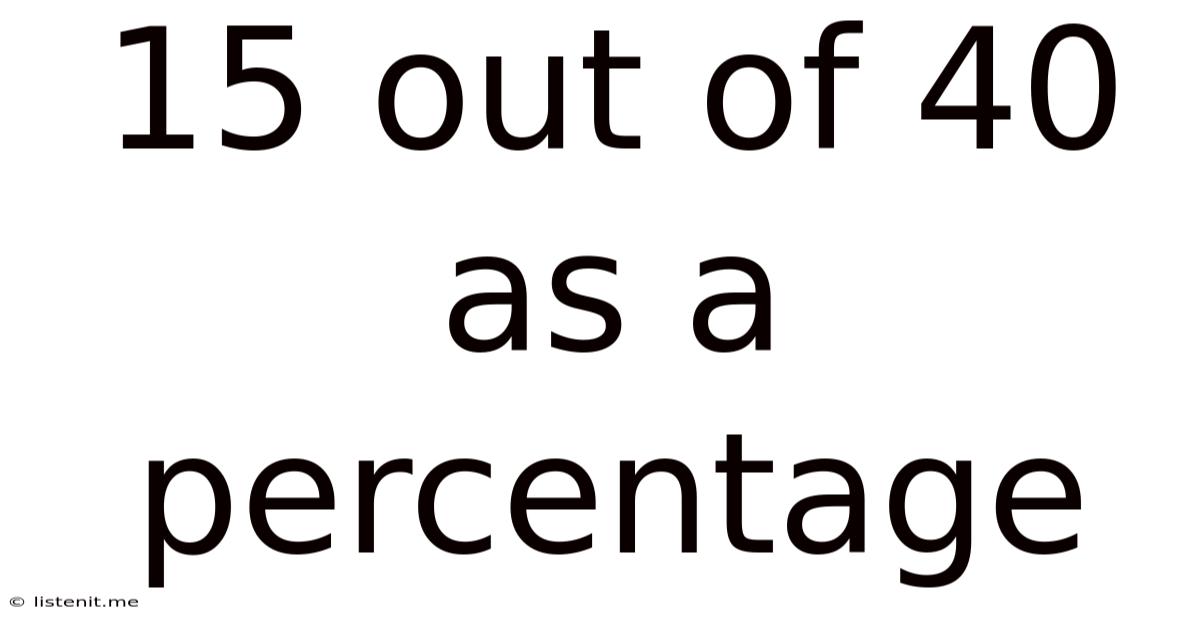
Table of Contents
15 out of 40 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the calculation of 15 out of 40 as a percentage, providing multiple methods and exploring the broader context of percentage calculations. We’ll also touch upon practical applications and common pitfalls to avoid.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (per centum). Percentages are a convenient way to represent proportions and comparisons, making data easier to understand and interpret.
For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5 in decimal form. Understanding this fundamental concept is crucial for tackling percentage calculations.
Calculating 15 out of 40 as a Percentage: Three Methods
There are several ways to calculate 15 out of 40 as a percentage. Let's explore three common methods:
Method 1: Using the Fraction Method
This is arguably the most straightforward method. We can express "15 out of 40" as a fraction: 15/40. To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100.
-
Simplify the fraction: Both 15 and 40 are divisible by 5, simplifying the fraction to 3/8.
-
Convert to a percentage: To obtain a denominator of 100, we can set up a proportion:
3/8 = x/100
Cross-multiply: 8x = 300
Solve for x: x = 300/8 = 37.5
Therefore, 15 out of 40 is 37.5%.
Method 2: Using the Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100.
-
Convert the fraction to a decimal: Divide 15 by 40: 15 ÷ 40 = 0.375
-
Multiply by 100 to get the percentage: 0.375 x 100 = 37.5%
Therefore, 15 out of 40 is 37.5%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 15 by 40 and then multiply the result by 100. The calculator will directly provide the percentage: 37.5%.
Practical Applications of Percentage Calculations
Understanding percentage calculations has wide-ranging applications in various fields:
-
Finance: Calculating interest rates, discounts, profit margins, taxes, and investment returns. For example, understanding the percentage increase or decrease in your investment portfolio is crucial for financial planning.
-
Retail: Determining sale prices, calculating markups, and analyzing sales data. A retailer uses percentages to understand the success of sales promotions and to adjust pricing strategies accordingly.
-
Education: Assessing student performance on tests and assignments. Grades are often expressed as percentages, providing a clear representation of a student's understanding of the subject matter.
-
Science: Representing data in graphs and charts, expressing experimental results, and calculating statistical probabilities. Percentages are crucial for visualizing and interpreting scientific data.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of ingredients in recipes, and understanding sales tax rates. Percentages are an essential part of our daily lives.
Common Mistakes to Avoid When Calculating Percentages
Several common errors can occur when working with percentages. Being aware of these pitfalls can help ensure accuracy:
-
Incorrect order of operations: Remember that multiplication and division should be performed before addition and subtraction. This is crucial when performing multi-step percentage calculations.
-
Confusing percentage increase and decrease: A 10% increase is not the same as a 10% decrease. The base value changes in each scenario. Understanding the difference is critical for accurate calculations.
-
Incorrectly interpreting percentage points: A change from 20% to 30% is a 10 percentage point increase, not a 50% increase. This distinction is important for avoiding misinterpretations of data.
-
Rounding errors: Rounding intermediate results can lead to accumulating errors. It's best to keep as many decimal places as possible during calculations and round only the final result.
-
Using the wrong formula: Ensure you are using the correct formula for the specific percentage calculation you need to perform.
Beyond the Basics: Advanced Percentage Concepts
While calculating 15 out of 40 as a percentage is a fundamental task, understanding more advanced concepts can be beneficial:
-
Percentage change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100.
-
Percentage point change: As mentioned earlier, this represents the absolute difference between two percentages.
-
Compound interest: This calculates interest earned on both the principal amount and accumulated interest. Understanding compound interest is essential for long-term financial planning.
-
Percentage yield: This is used in investment and finance to represent the return on an investment relative to its initial cost.
-
Weighted averages: These calculations give different weights to different values, reflecting their relative importance.
Improving Your Percentage Calculation Skills
Practice is key to mastering percentage calculations. Regularly solving different types of percentage problems will help you improve your skills and develop a deeper understanding of the concepts. You can find numerous practice problems online or in textbooks. Using different methods for the same problem can also reinforce your understanding and identify any areas where you need improvement.
Conclusion: The Importance of Percentage Literacy
The ability to calculate and interpret percentages is a valuable life skill. From managing personal finances to understanding complex data, percentage literacy empowers you to make informed decisions and navigate the world more effectively. While calculating 15 out of 40 as a percentage might seem like a simple task, it forms the foundation for understanding and applying broader percentage concepts in various aspects of life and work. Mastering this fundamental skill opens doors to more complex and rewarding challenges. Remember to practice regularly, and soon, you’ll be a percentage pro!
Latest Posts
Latest Posts
-
1 Day 3 Hours From Now
May 25, 2025
-
How Many Calories Should I Eat If I Weigh 240
May 25, 2025
-
What Is 5 8 As A Fraction
May 25, 2025
-
Write The Prime Factorization Of 70
May 25, 2025
-
What Is The Prime Factorization Of 116
May 25, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.