130 Of What Number Is 52
listenit
May 09, 2025 · 4 min read
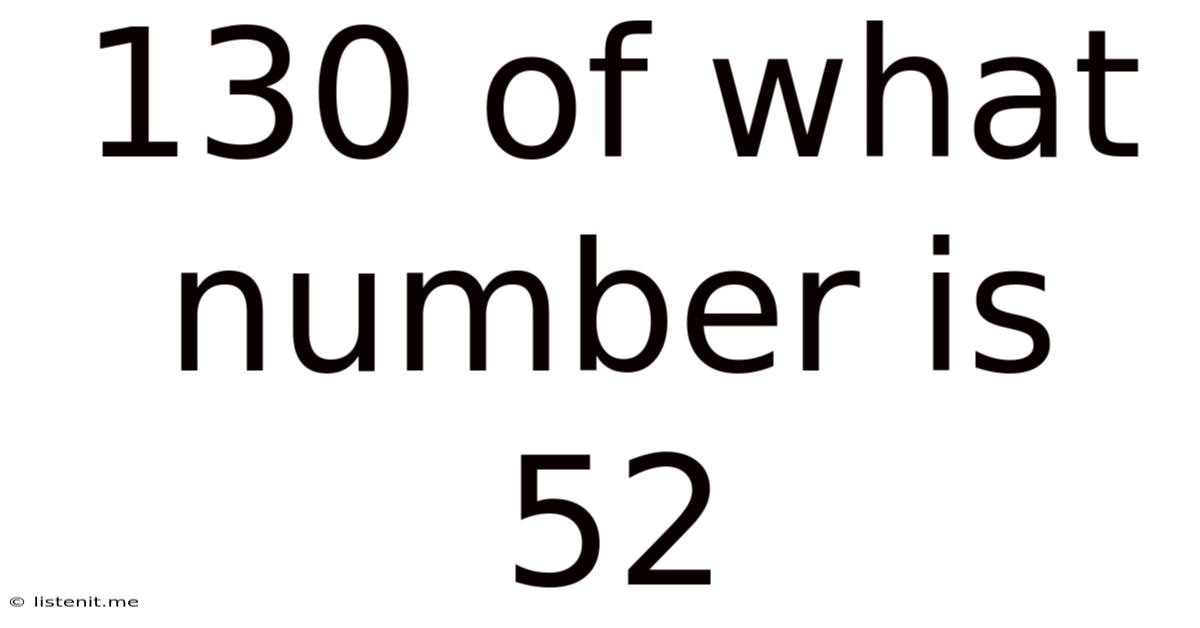
Table of Contents
130% of What Number is 52? A Deep Dive into Percentage Calculations
Finding the base number when you know a percentage and the resulting value is a common mathematical problem encountered in various fields, from finance and business to everyday life. This article explores the question: "130% of what number is 52?" We'll not only solve this specific problem but also delve into the underlying principles of percentage calculations, providing you with the tools to tackle similar problems independently. We'll cover different methods, explain the reasoning behind each step, and even look at real-world applications.
Understanding Percentages
Before tackling the problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" is used to denote percentage. For example, 50% represents 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding percentages is crucial in various contexts:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data proportions and trends.
- Science: Expressing concentrations of solutions or experimental results.
- Everyday Life: Calculating tips, sales discounts, and understanding proportions in recipes.
Method 1: Algebraic Approach
This method involves setting up an equation and solving for the unknown variable. Let's represent the unknown number as 'x'. The problem "130% of what number is 52" can be translated into the following equation:
1.30x = 52
To solve for 'x', we divide both sides of the equation by 1.30:
x = 52 / 1.30
x = 40
Therefore, 130% of 40 is 52.
Method 2: Proportion Method
This method utilizes the concept of proportions. We can set up a proportion where one ratio represents the percentage (130/100) and the other ratio represents the given value (52/x), where 'x' is the unknown number. The proportion is:
130/100 = 52/x
To solve for 'x', we cross-multiply:
130x = 5200
Now, divide both sides by 130:
x = 5200 / 130
x = 40
Again, we arrive at the same answer: 130% of 40 is 52.
Method 3: Using Decimal Equivalents
This method converts the percentage into its decimal equivalent before performing the calculation. 130% is equivalent to 1.30 (130 divided by 100). The problem becomes:
1.30 * x = 52
Solving for 'x':
x = 52 / 1.30
x = 40
This method yields the same result: 130% of 40 is 52.
Verifying the Solution
Let's verify our answer by calculating 130% of 40:
(130/100) * 40 = 1.30 * 40 = 52
Our calculation confirms that 40 is indeed the correct answer.
Real-World Applications
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
Finance:
- Investment Returns: If an investment increased by 130%, and the final value is $52,000, the initial investment was $40,000.
- Sales Tax: If a product costs $40 before tax, and the sales tax is 30%, the total cost after tax would be $52.
- Discounts: If an item is discounted by 30%, and the final price is $40, the original price was approximately $52 (This situation requires a slight adjustment to the formula).
Business:
- Profit Margins: If a company’s profit margin is 130% and they made a profit of $52, the cost of goods sold was $40. (Note: A 130% profit margin suggests a significant markup beyond standard models; this may indicate a specific pricing strategy).
- Sales Growth: If sales increased by 130% and reached $52 million, the original sales figure was $40 million.
- Market Share: If a company holds a 130% increase in market share over the previous quarter, representing 52% of total market share. This would imply market share growth over previous data points. Further investigation into how this exceeds 100% is required for an accurate interpretation.
Everyday Life:
- Recipe Scaling: If a recipe calls for 40 grams of flour and you want to increase it by 130%, you would use 52 grams.
- Tip Calculation: If a 130% tip (an incredibly generous tip!) on a meal costs $52, the meal cost $40.
Handling Percentages Greater Than 100%
It's important to note that percentages can be greater than 100%. This signifies an increase beyond the original value. For example, a 130% increase means the final value is 130% of the original value, which is equivalent to 230% of the original value.
Common Mistakes to Avoid
- Incorrect Decimal Conversion: Ensure you correctly convert percentages to decimals before performing calculations. 130% should be converted to 1.30, not 0.13.
- Mixing up the Values: Keep track of which value represents the percentage, the base number, and the resulting value.
- Incorrect Equation Setup: Double-check that your equation accurately reflects the problem statement.
Conclusion
Solving problems involving percentages requires a clear understanding of the underlying principles. We've demonstrated three methods—algebraic, proportional, and using decimal equivalents—to solve the problem "130% of what number is 52?" The answer, 40, was verified using all methods. By mastering these techniques, you'll be equipped to handle various percentage calculations confidently in various real-world applications. Remember to always double-check your work and consider the context of the problem to ensure your interpretation of the results is accurate. The ability to work with percentages efficiently is a valuable skill applicable in numerous aspects of life and work.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 10 And 20
May 11, 2025
-
How To Find If A Triangle Is Right
May 11, 2025
-
What Percent Is 36 Out Of 45
May 11, 2025
-
An Atom With An Electrical Charge Is An
May 11, 2025
-
80 Expressed As A Fraction Is
May 11, 2025
Related Post
Thank you for visiting our website which covers about 130 Of What Number Is 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.