What Percent Is 36 Out Of 45
listenit
May 11, 2025 · 5 min read
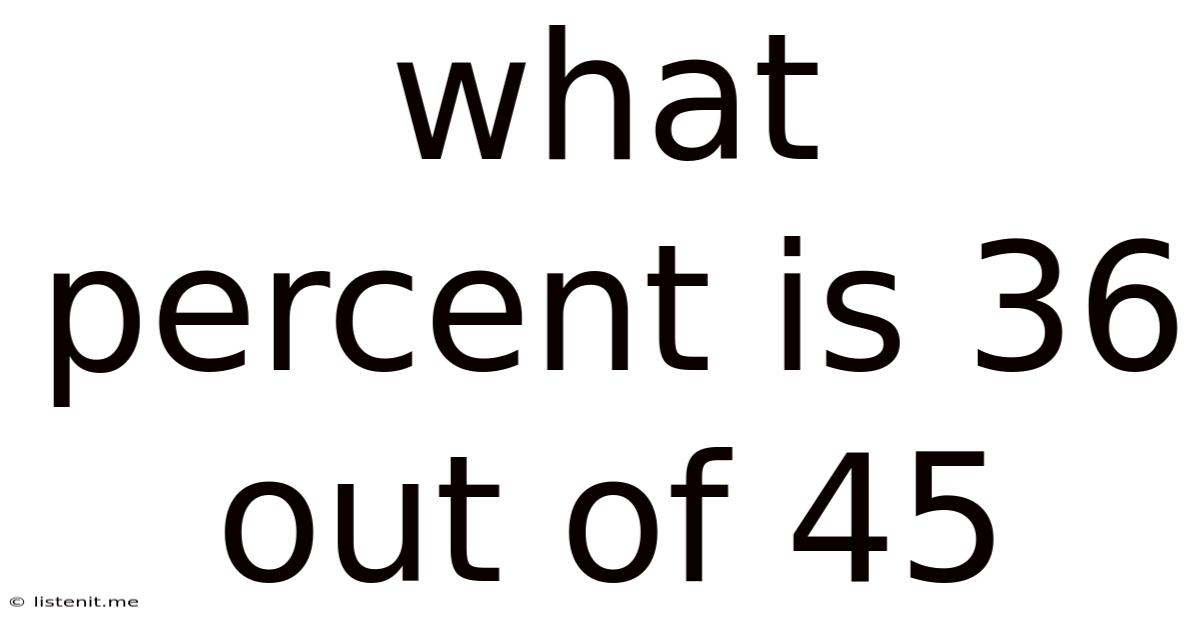
Table of Contents
What Percent is 36 out of 45? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percent one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will not only answer the question "What percent is 36 out of 45?" but also delve into the underlying principles of percentage calculations, providing you with a robust understanding of this essential mathematical concept.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred," and it's denoted by the symbol "%". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to compare proportions and express ratios, making them widely used in various fields.
Calculating "What Percent is 36 out of 45?"
To find what percent 36 is of 45, we need to follow a simple three-step process:
Step 1: Set up the Fraction
First, represent the problem as a fraction. The number we want to express as a percentage (36) becomes the numerator, and the total number (45) becomes the denominator:
36/45
Step 2: Convert the Fraction to a Decimal
Next, we convert the fraction to a decimal by dividing the numerator by the denominator:
36 ÷ 45 = 0.8
Step 3: Convert the Decimal to a Percentage
Finally, we convert the decimal to a percentage by multiplying it by 100 and adding the "%" symbol:
0.8 x 100 = 80%
Therefore, 36 is 80% of 45.
Different Methods for Calculating Percentages
While the above method is straightforward, there are alternative approaches to calculating percentages, each with its own advantages depending on the context and the tools available.
Method 2: Using Proportions
This method involves setting up a proportion where x represents the unknown percentage:
x/100 = 36/45
To solve for x, we cross-multiply:
45x = 3600
x = 3600/45
x = 80
Therefore, x = 80%. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply enter 36, press the division symbol, enter 45, press the equals sign, and then multiply by 100. The result will be 80%. This method is efficient and minimizes the risk of manual calculation errors.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
1. Finance and Budgeting:
- Calculating discounts: Determining the final price after a percentage discount. For example, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
- Interest calculations: Computing simple and compound interest on loans or investments.
- Tax calculations: Determining the amount of tax payable on income or purchases.
- Analyzing financial statements: Understanding profit margins, return on investment (ROI), and other key financial metrics.
2. Retail and Sales:
- Calculating profit margins: Determining the percentage of profit made on each sale.
- Tracking sales performance: Analyzing sales figures to assess the effectiveness of marketing campaigns and pricing strategies.
- Calculating markups: Determining the selling price by adding a percentage markup to the cost price.
3. Science and Statistics:
- Analyzing experimental data: Expressing results as percentages to facilitate comparisons and draw conclusions.
- Calculating statistical measures: Determining percentages in various statistical analyses, such as calculating the percentage of respondents who agree with a particular statement in a survey.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount at restaurants.
- Understanding nutrition labels: Interpreting the percentage of daily recommended values for nutrients in food products.
- Comparing prices: Determining which product offers better value for money based on unit price or percentage discounts.
Advanced Percentage Calculations
Beyond the basic calculations, understanding more complex percentage problems is crucial for a thorough grasp of this concept.
1. Percentage Increase and Decrease
Calculating percentage increase or decrease involves comparing two numbers to determine the percentage change. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100
For example, if a product's price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100 = 20%
2. Finding the Original Value
Sometimes, you know the percentage and the final value but need to determine the original value. This requires working backward using algebraic techniques.
For example, if a product is on sale for $70 after a 30% discount, the original price (x) can be calculated as follows:
x - 0.3x = 70
0.7x = 70
x = 70 / 0.7
x = 100
The original price was $100.
3. Percentage Points vs. Percentage Change
It's important to distinguish between percentage points and percentage change. Percentage points represent the absolute difference between two percentages, while percentage change represents the relative change. For example, if interest rates increase from 2% to 5%, the increase is 3 percentage points, but the percentage change is a 150% increase [(5-2)/2 * 100].
Mastering Percentage Calculations: Tips and Tricks
To become proficient in percentage calculations, consider these helpful tips:
- Practice regularly: The more you practice, the more comfortable you'll become with the concepts and methods.
- Use different methods: Try various approaches to solve percentage problems to find the method that works best for you.
- Understand the underlying principles: Focus on grasping the core concepts rather than just memorizing formulas.
- Utilize online resources: Numerous online calculators and tutorials can aid your learning and provide additional practice problems.
- Break down complex problems: Divide complex problems into smaller, manageable steps to simplify the process.
By understanding the principles behind percentage calculations and practicing regularly, you can confidently tackle a wide range of problems involving percentages, both simple and complex. This skill is invaluable in various aspects of life, making it a worthwhile investment of your time and effort. Remember, mastering percentages isn't just about getting the right answer; it's about developing a deeper understanding of proportional relationships and their applications in the real world.
Latest Posts
Latest Posts
-
Average Human Reaction Time In Seconds
May 12, 2025
-
Where Is The Most Mass Of An Atom
May 12, 2025
-
Molar Mass Of Air In Kg Mol
May 12, 2025
-
How To Clear Fractions From Equations
May 12, 2025
-
What Is The Molecule That Stores Energy
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 36 Out Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.