110 Out Of 200 As A Percentage
listenit
May 25, 2025 · 5 min read
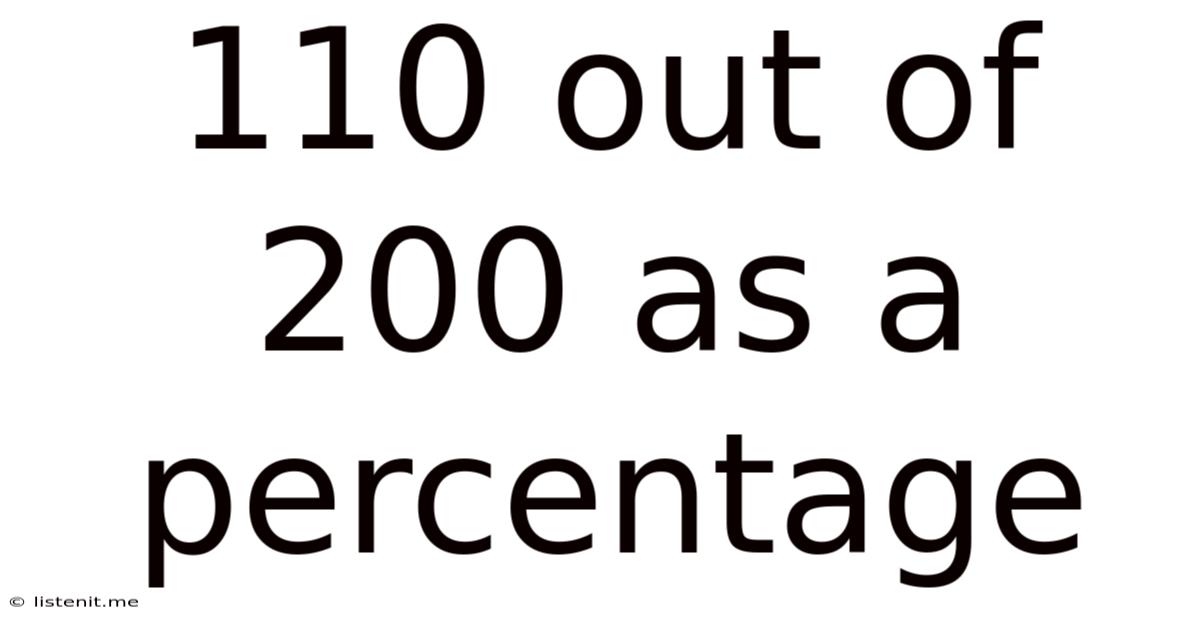
Table of Contents
110 out of 200 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in numerous aspects of life, from academic pursuits to professional settings. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide will delve into the calculation of 110 out of 200 as a percentage, exploring different methods and highlighting their applications. We will also examine related concepts and practical examples to solidify your understanding.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Percentages are commonly used to represent proportions, rates, and changes. For instance, a 25% discount indicates that you'll pay 75% of the original price. Understanding percentages allows you to quickly grasp the relative size of one quantity compared to another.
Calculating 110 out of 200 as a Percentage: The Basic Method
The most straightforward way to calculate 110 out of 200 as a percentage involves three simple steps:
-
Form a fraction: Express the given numbers as a fraction: 110/200.
-
Convert the fraction to a decimal: Divide the numerator (110) by the denominator (200): 110 ÷ 200 = 0.55
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.55 x 100 = 55%.
Therefore, 110 out of 200 is 55%.
Alternative Calculation Methods
While the basic method is perfectly adequate, other approaches can be equally effective, especially when dealing with more complex scenarios or when performing mental calculations.
Method 2: Simplifying the Fraction
Before converting to a decimal, you can simplify the fraction 110/200 by finding the greatest common divisor (GCD) of 110 and 200. The GCD of 110 and 200 is 10. Dividing both the numerator and the denominator by 10 simplifies the fraction to 11/20.
Now, convert 11/20 to a decimal: 11 ÷ 20 = 0.55
Finally, convert the decimal to a percentage: 0.55 x 100 = 55%
This method demonstrates that simplifying the fraction first can sometimes make the calculation easier.
Method 3: Using Proportions
Another approach involves setting up a proportion. Let 'x' represent the percentage we're trying to find. We can write the proportion as:
110/200 = x/100
To solve for 'x', cross-multiply:
200x = 11000
Divide both sides by 200:
x = 55
Therefore, 110 out of 200 is 55%. This method is particularly useful when dealing with more complex percentage problems.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has widespread applications across various domains:
1. Academic Performance
Students frequently encounter percentage calculations when determining their grades. If a student scores 110 out of 200 on an exam, their percentage score is 55%, which helps to gauge their performance relative to the total possible marks.
2. Business and Finance
In business, percentages are used extensively for:
- Profit margins: Calculating the percentage of profit relative to revenue.
- Discount rates: Determining price reductions for promotional offers.
- Interest rates: Calculating the cost of borrowing money or the return on investments.
- Market share: Assessing a company's share of the total market.
3. Data Analysis and Statistics
Percentages are fundamental to data analysis and statistics for representing proportions within datasets, allowing for clear visualization and interpretation of trends and patterns. For instance, if 110 out of 200 respondents in a survey answered "yes" to a question, it represents 55% of the respondents.
4. Everyday Life
Percentage calculations are prevalent in daily life scenarios, including:
- Calculating tips: Determining the appropriate amount to tip at a restaurant.
- Understanding sales taxes: Computing the total cost of an item including tax.
- Comparing prices: Evaluating the best value for money when comparing products.
Beyond the Basics: Exploring Related Concepts
Understanding percentages extends beyond simple calculations. Let's explore some related concepts that build upon this foundational knowledge:
Percentage Increase and Decrease
Percentage increase or decrease shows the relative change between two values. For instance, if a price increases from 100 to 155, the percentage increase is calculated as follows:
- Find the difference: 155 - 100 = 55
- Divide the difference by the original value: 55/100 = 0.55
- Multiply by 100 to express as a percentage: 0.55 x 100 = 55%
Therefore, the price increased by 55%. Similarly, you can calculate percentage decrease.
Percentage Points
It's crucial to distinguish between percentage points and percentage change. A change from 40% to 45% is a 5 percentage point increase, but it's a 12.5% increase ( (5/40) * 100). Understanding this distinction is crucial for interpreting statistical data accurately.
Advanced Applications and Problem Solving
Let's consider more complex scenarios involving percentage calculations:
Example 1: A store offers a 20% discount on an item originally priced at $200. What is the discounted price?
- Calculate the discount amount: 20% of $200 = (20/100) * $200 = $40
- Subtract the discount from the original price: $200 - $40 = $160
The discounted price is $160.
Example 2: A company's revenue increased from $100,000 to $155,000. What is the percentage increase?
- Find the difference: $155,000 - $100,000 = $55,000
- Divide the difference by the original revenue: $55,000 / $100,000 = 0.55
- Multiply by 100 to express as a percentage: 0.55 x 100 = 55%
The company's revenue increased by 55%.
Example 3: If 55% of a class of 200 students passed an exam, how many students passed?
- Convert the percentage to a decimal: 55% = 0.55
- Multiply the decimal by the total number of students: 0.55 * 200 = 110
110 students passed the exam.
Conclusion: Mastering Percentage Calculations
Calculating 110 out of 200 as a percentage, resulting in 55%, is a fundamental skill applicable in numerous contexts. This guide has explored different methods for calculating percentages, highlighting their practical applications across various fields. Mastering percentage calculations equips you with a valuable tool for interpreting data, making informed decisions, and effectively communicating numerical information. Remember to apply the concepts of percentage increase, decrease, and percentage points to fully grasp the nuances of percentage calculations and solve more complex problems. With practice and a solid understanding of the underlying principles, you'll confidently tackle any percentage-related challenge.
Latest Posts
Latest Posts
-
12 5 Is 8 Of What Number
May 25, 2025
-
What Is The Greatest Common Factor Of 30 And 36
May 25, 2025
-
411 Rounded To The Nearest Hundred
May 25, 2025
-
What Is 9 Months From November
May 25, 2025
-
What Is 30 Of 60 Dollars
May 25, 2025
Related Post
Thank you for visiting our website which covers about 110 Out Of 200 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.