12.5 Is 8 Of What Number
listenit
May 25, 2025 · 4 min read
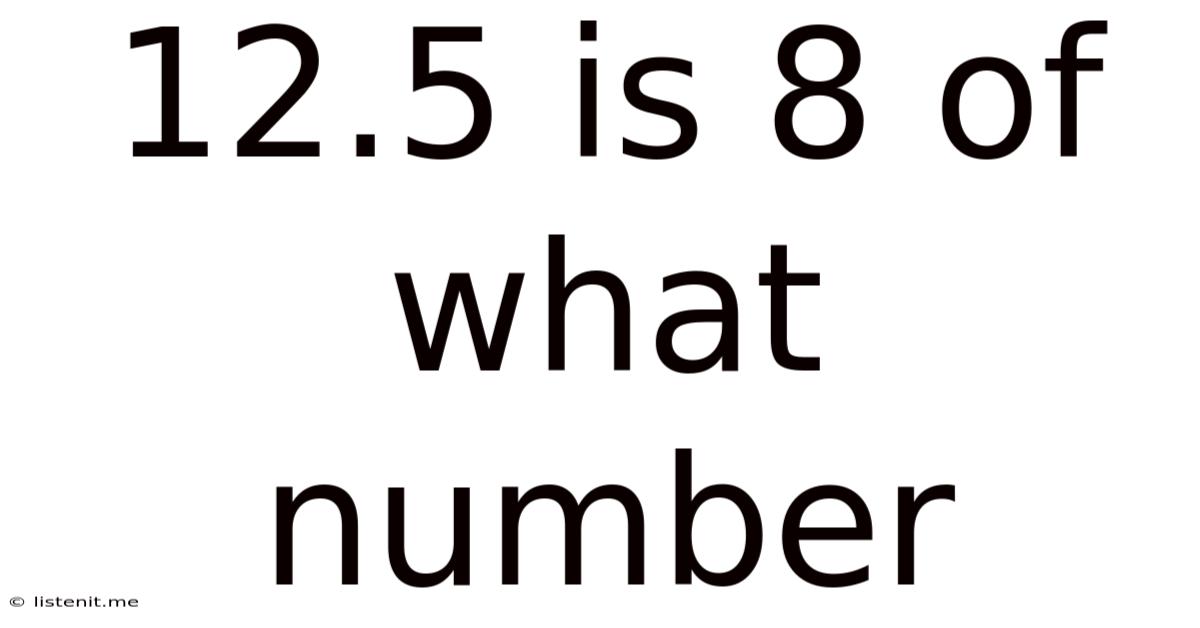
Table of Contents
12.5 is 8% of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to analyzing data and making financial decisions. This article delves into the solution of the problem "12.5 is 8% of what number?", exploring the different methods to arrive at the answer and providing a broader understanding of percentage calculations. We'll break down the process step-by-step, making it accessible to everyone, regardless of their mathematical background.
Understanding the Problem: Deconstructing "12.5 is 8% of What Number?"
The question "12.5 is 8% of what number?" presents a classic percentage problem. We're given a part (12.5), a percentage (8%), and we need to find the whole number (the unknown). This type of problem requires us to work backward from the percentage to find the original value.
This problem is frequently encountered in various contexts:
- Financial calculations: Determining the original price before a discount.
- Data analysis: Finding the total based on a percentage representation.
- Statistical interpretations: Calculating the whole population based on a sample percentage.
Method 1: Using the Percentage Formula
The most straightforward approach involves using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part = 12.5
- Percentage = 8% = 0.08 (remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (this is the unknown we need to find)
Substituting these values into the formula gives us:
12.5 = 0.08x
To solve for 'x', we divide both sides of the equation by 0.08:
x = 12.5 / 0.08
x = 156.25
Therefore, 12.5 is 8% of 156.25.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
8/100 = 12.5/x
This proportion reads: "8 is to 100 as 12.5 is to x."
To solve for x, we cross-multiply:
8x = 12.5 * 100
8x = 1250
x = 1250 / 8
x = 156.25
Again, we arrive at the same answer: 12.5 is 8% of 156.25.
Method 3: Working with Fractions
Percentages can also be expressed as fractions. 8% can be written as 8/100, which simplifies to 2/25. We can then set up an equation:
(2/25) * x = 12.5
To solve for x, we multiply both sides by the reciprocal of 2/25, which is 25/2:
x = 12.5 * (25/2)
x = 156.25
This method confirms our previous results: 12.5 is 8% of 156.25.
Verifying the Answer
It's always a good practice to verify your answer. Let's check if 8% of 156.25 is indeed 12.5:
0.08 * 156.25 = 12.5
The calculation confirms our solution is correct.
Expanding the Understanding: Working with Different Percentages and Values
The methods described above can be applied to solve any percentage problem where you know the part and the percentage, and need to find the whole. Let's consider a few examples:
Example 1: 20 is 25% of what number?
Using the formula: 20 = 0.25x => x = 20 / 0.25 = 80
Example 2: 50 is 10% of what number?
Using the proportion method: 10/100 = 50/x => 10x = 5000 => x = 500
Practical Applications of Percentage Calculations
Percentage calculations are essential in numerous real-world scenarios:
- Sales and discounts: Calculating the original price of an item after a discount. For example, if a shirt is on sale for $25 after a 20% discount, you can use the methods above to determine the original price.
- Tax calculations: Determining the total amount payable after adding sales tax.
- Financial investments: Calculating returns on investments, interest earned, and compound interest.
- Statistical analysis: Interpreting survey results, understanding population demographics, and analyzing data trends.
Beyond the Basics: Advanced Percentage Problems
While the problem "12.5 is 8% of what number?" provides a foundation in percentage calculations, more complex problems may involve multiple percentages, consecutive discounts, or percentage increases over time. These problems often require a multi-step approach, combining the fundamental principles discussed above.
Tips for Success in Percentage Calculations
- Convert percentages to decimals: Always convert percentages to their decimal equivalents (by dividing by 100) before performing calculations.
- Use consistent units: Ensure that all values are expressed in the same units.
- Check your work: Always verify your answer to ensure accuracy.
- Practice regularly: The more you practice percentage calculations, the more comfortable and proficient you will become.
Conclusion: Mastering the Art of Percentage Calculations
Understanding and mastering percentage calculations is crucial for navigating various aspects of daily life and professional endeavors. The problem "12.5 is 8% of what number?" serves as an excellent illustration of the fundamental principles involved. By applying the methods discussed—using the percentage formula, proportions, or fractions—you can effectively solve this and similar problems. Consistent practice and a clear understanding of the underlying concepts will empower you to confidently tackle any percentage-related challenge. Remember, the key is to break down the problem into manageable steps and to always verify your answer.
Latest Posts
Latest Posts
-
What Is Three Hours From Now
May 26, 2025
-
What Is 1 3 Of 4000
May 26, 2025
-
Least Common Multiple Of 21 And 49
May 26, 2025
-
What Is The Date 40 Weeks From Today
May 26, 2025
-
15 Feet Per Second To Mph
May 26, 2025
Related Post
Thank you for visiting our website which covers about 12.5 Is 8 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.