11 X 11 - 6 X 17 + 4
listenit
May 24, 2025 · 5 min read
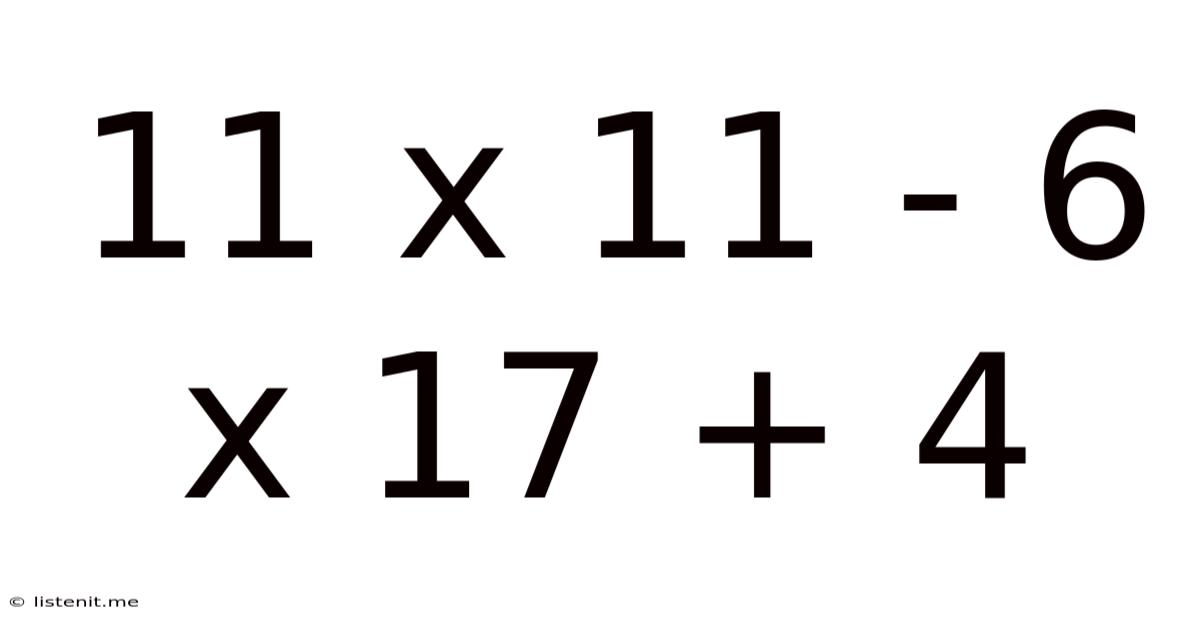
Table of Contents
Decoding the Mathematical Expression: 11 x 11 - 6 x 17 + 4
This seemingly simple mathematical expression, 11 x 11 - 6 x 17 + 4, offers a fascinating opportunity to explore the order of operations, delve into the properties of numbers, and even touch upon the broader context of mathematical notation and its historical evolution. While the solution itself is straightforward, the process of reaching it and understanding its underlying principles is where the true learning lies. This article will dissect this expression step-by-step, explaining the reasoning behind each calculation and exploring related mathematical concepts.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before we begin solving the expression, it's crucial to understand the order of operations. This set of rules dictates the sequence in which mathematical operations should be performed to obtain the correct result. This is often remembered by acronyms like PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same fundamental concept.
In our expression, 11 x 11 - 6 x 17 + 4, there are no parentheses or exponents. Therefore, we proceed with multiplication and division first, from left to right, followed by addition and subtraction, also from left to right.
Step-by-Step Solution
Let's break down the solution step-by-step:
-
11 x 11: This is the first multiplication operation. 11 multiplied by 11 equals 121. Our expression now becomes: 121 - 6 x 17 + 4
-
6 x 17: This is the next multiplication operation. 6 multiplied by 17 equals 102. Our expression now becomes: 121 - 102 + 4
-
121 - 102: This is the first subtraction operation. 121 minus 102 equals 19. Our expression now becomes: 19 + 4
-
19 + 4: This is the final addition operation. 19 plus 4 equals 23.
Therefore, the solution to the expression 11 x 11 - 6 x 17 + 4 is 23.
Exploring the Components: Numbers and Operations
Let's delve deeper into the individual components of the expression:
The Numbers:
-
11: An integer, a prime number, and a composite number (though it is only composed of 1 and itself). It's a relatively small number with significant historical and cultural relevance.
-
6: Another integer, a composite number (2 x 3). It's an even number, and has various mathematical properties, like being a perfect number (sum of its divisors = 1 + 2 + 3 = 6).
-
17: An integer, a prime number. Prime numbers, like 17, only have two divisors: 1 and itself. They are fundamental building blocks of number theory.
-
4: An integer, a composite number (2 x 2), a perfect square (2²). It is also an even number and holds significance in geometry (squares, etc).
The Operations:
-
Multiplication (x): A fundamental arithmetic operation representing repeated addition. It's commutative (a x b = b x a) and associative (a x (b x c) = (a x b) x c).
-
Subtraction (-): Another fundamental arithmetic operation representing the inverse of addition. It is not commutative (a - b ≠ b - a) and not associative (a - (b - c) ≠ (a - b) - c).
-
Addition (+): A fundamental arithmetic operation representing the combining of quantities. It's commutative (a + b = b + a) and associative (a + (b + c) = (a + b) + c).
Expanding the Context: Mathematical Notation and History
The seemingly simple notation we use today—the symbols for numbers, operations, and the order of operations—is the result of centuries of evolution. Different civilizations developed various systems of notation, and the standardization we enjoy today is a relatively recent development. Understanding this historical context helps appreciate the power and elegance of modern mathematical notation.
Early forms of mathematical notation relied heavily on words and symbols that were not universally understood. The development of Arabic numerals and the standardization of symbols for operations greatly simplified mathematical communication and calculation. The order of operations itself, while now seemingly intuitive, was codified over time to ensure consistency and avoid ambiguity in complex calculations.
Applications and Further Exploration
This seemingly simple expression, and the principles it demonstrates, have far-reaching applications across various fields:
-
Computer Programming: Order of operations is fundamental in programming, ensuring that calculations are performed correctly within computer code.
-
Engineering and Physics: Complex calculations involving multiple operations are commonplace in engineering and physics, requiring a thorough understanding of the order of operations and mathematical principles.
-
Data Analysis and Statistics: Statistical analysis often involves numerous calculations, relying on the accuracy of mathematical operations and the correct application of the order of operations.
-
Financial Modeling: Financial models often utilize complex mathematical formulas that require a strong understanding of order of operations for accurate financial projections.
Beyond the Basics: Exploring More Complex Expressions
This simple expression can be a stepping stone to exploring much more complex mathematical expressions. For instance, we can introduce:
-
Parentheses: Adding parentheses changes the order of operations significantly. For example, (11 x 11) - (6 x 17) + 4 would yield a different result.
-
Exponents: Including exponents would add another layer of complexity, requiring an understanding of exponential functions and their properties.
-
Variables: Introducing variables (e.g., x, y, z) would lead into algebraic expressions and equations, opening up a whole new realm of mathematical exploration.
Conclusion
The expression 11 x 11 - 6 x 17 + 4 may seem simple at first glance, but it serves as a microcosm of fundamental mathematical concepts. By carefully examining its solution, we’ve uncovered the importance of the order of operations, explored the properties of numbers, and touched upon the historical development of mathematical notation. Understanding these principles forms a solid foundation for more advanced mathematical studies and applications across numerous fields. The seemingly simple act of solving this expression reveals the elegance and power inherent within mathematics, illustrating how fundamental principles underpin complex systems and calculations. Continuing to explore and expand upon this foundational understanding will unlock further insights into the fascinating world of mathematics.
Latest Posts
Latest Posts
-
What Percent Is 20 Out Of 23
May 25, 2025
-
11 Out Of 17 As A Percentage
May 25, 2025
-
How Many Days Away Is March 7
May 25, 2025
-
What Is The Prime Factorization Of 71
May 25, 2025
-
What Is The Greatest Common Factor Of 48 And 42
May 25, 2025
Related Post
Thank you for visiting our website which covers about 11 X 11 - 6 X 17 + 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.