1000 Is 30 Percent Of What Number
listenit
May 25, 2025 · 5 min read
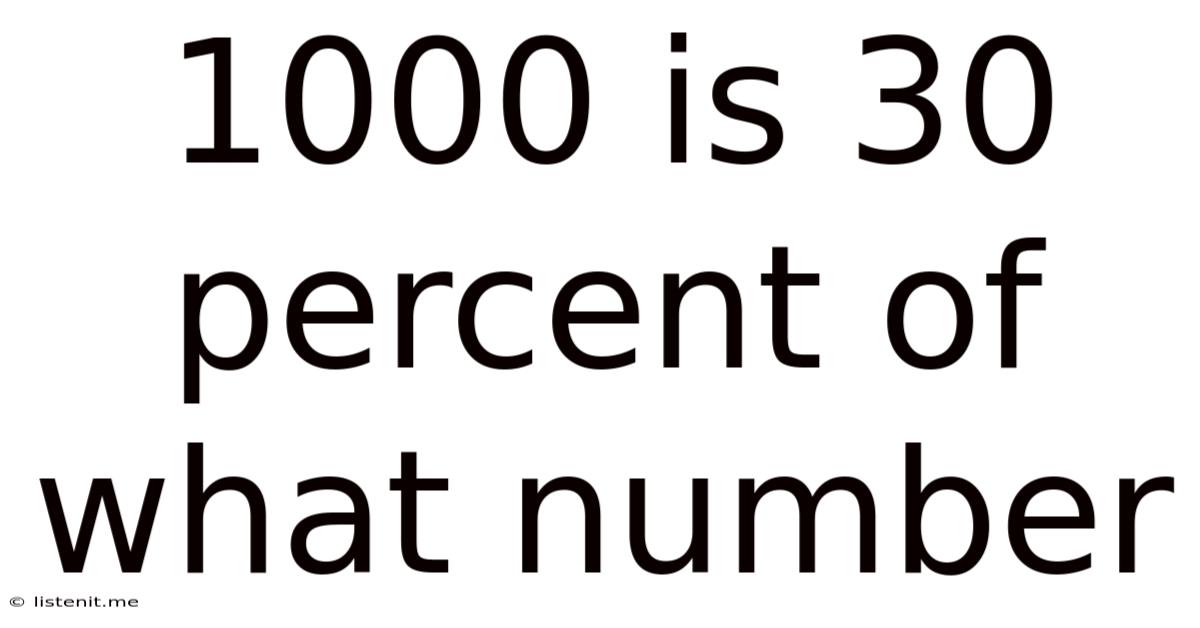
Table of Contents
1000 is 30 Percent of What Number? Unraveling the Math and its Real-World Applications
Finding an unknown number when you know a percentage of it is a common mathematical problem. This article delves into how to solve "1000 is 30 percent of what number," explaining the process step-by-step, exploring different solution methods, and showcasing real-world applications where this type of calculation proves invaluable. We will also discuss the importance of understanding percentages and their role in various fields.
Understanding the Problem
The core of the problem lies in understanding the relationship between a percentage, a part, and the whole. We are given that 1000 represents 30% of a larger, unknown number. Our goal is to determine this unknown whole. This is a fundamental concept in percentage calculations, and mastering it unlocks the ability to solve a wide array of problems in finance, statistics, and everyday life.
Method 1: Using the Percentage Formula
The most straightforward method uses the basic percentage formula:
Part = Percentage × Whole
In our case:
- Part = 1000
- Percentage = 30% = 0.30 (Remember to convert percentages to decimals by dividing by 100)
- Whole = x (this is the unknown number we need to find)
Substituting these values into the formula gives us:
1000 = 0.30x
To solve for x (the whole), we divide both sides of the equation by 0.30:
x = 1000 / 0.30
x ≈ 3333.33
Therefore, 1000 is 30% of approximately 3333.33.
Method 2: Using Proportions
Another approach involves setting up a proportion. We can express the problem as a ratio:
1000 / x = 30 / 100
This proportion states that the ratio of the part (1000) to the whole (x) is equal to the ratio of the percentage (30) to 100 (representing the whole percentage).
To solve for x, we cross-multiply:
1000 * 100 = 30 * x
100000 = 30x
Divide both sides by 30:
x = 100000 / 30
x ≈ 3333.33
This method confirms our previous result: 1000 is 30% of approximately 3333.33.
Method 3: Working Backwards from the Percentage
We can also think of this problem as working backward from the percentage. If 30% is 1000, then 1% would be 1000/30. To find the whole (100%), we multiply this value by 100:
1% = 1000 / 30 ≈ 33.33
100% = (1000 / 30) * 100 ≈ 3333.33
Again, this method arrives at the same solution: approximately 3333.33.
Real-World Applications: Where Percentage Calculations Matter
Understanding how to solve problems like "1000 is 30 percent of what number" is crucial in many real-world scenarios. Let's explore some examples:
1. Business and Finance:
- Profit Margins: A company might know that it made a profit of $1000, representing 30% of its revenue. This calculation helps them determine the total revenue generated.
- Sales Targets: Sales teams often have targets expressed as percentages. If a team needs to achieve 30% of a yearly sales goal ($1000 is the 30% achieved so far), they can calculate the total annual target.
- Investment Returns: Investors use percentage calculations to track their returns. If an investment yielded a 30% return of $1000, this method finds the initial investment amount.
- Discounts and Sales: A store offers a 30% discount resulting in a $1000 saving. This calculation helps determine the original price of the item.
2. Data Analysis and Statistics:
- Sampling: In statistical surveys, a sample might represent a certain percentage of a larger population. Knowing the sample size and the percentage it represents helps estimate the size of the overall population.
- Data Interpretation: Percentage calculations are vital for interpreting data presented in charts, graphs, and reports. Understanding proportions is crucial in drawing meaningful conclusions.
3. Everyday Life:
- Tip Calculations: Calculating tips in restaurants often involves determining a percentage of the bill.
- Sales Tax: Understanding sales tax calculations requires finding percentages of prices.
- Recipe Adjustments: Scaling up or down recipes involves adjusting ingredients based on percentages.
4. Scientific Applications:
- Chemical Concentrations: In chemistry, concentrations are often expressed as percentages. Calculating the amount of a solute in a solution based on its concentration requires this type of calculation.
- Population Growth: Tracking population growth often utilizes percentage changes over time.
5. Engineering and Construction:
- Material Estimates: Engineers and construction professionals use percentage calculations to estimate material needs for projects, accounting for waste and other factors.
Importance of Mastering Percentage Calculations
The ability to solve percentage problems is a fundamental skill with widespread applicability. It significantly improves problem-solving capabilities in various professional and personal settings. Proficiency in this area contributes to:
- Improved Financial Literacy: Understanding percentages is vital for managing finances effectively, making informed decisions about investments, and interpreting financial reports.
- Enhanced Data Analysis Skills: Interpreting and analyzing data effectively is essential in today's data-driven world, and percentages form a crucial part of this process.
- Stronger Problem-Solving Abilities: Percentage calculations improve overall mathematical reasoning and analytical thinking, making individuals better equipped to tackle complex problems.
- Greater Confidence in Decision-Making: Understanding percentages enables informed decision-making across numerous aspects of life, from personal finance to professional projects.
Conclusion
The question "1000 is 30 percent of what number?" may seem simple, but it highlights a crucial mathematical concept with far-reaching real-world implications. By understanding the various methods to solve this type of problem and recognizing its practical applications, we can enhance our numerical literacy and improve our abilities in many areas of life. Mastering percentage calculations equips us to tackle more complex problems with confidence and makes us better equipped to navigate the data-rich world we inhabit. The ability to quickly and accurately calculate percentages is a valuable asset in various fields, and its importance should not be underestimated.
Latest Posts
Latest Posts
-
How Many 5 6 Are In 3
May 25, 2025
-
5 6 Divided By 3 As A Fraction
May 25, 2025
-
30 Days After May 14 2024
May 25, 2025
-
What Is The Least Common Multiple Of 21 And 24
May 25, 2025
-
What Is 20 Off Of 14 99
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1000 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.