5/6 Divided By 3 As A Fraction
listenit
May 25, 2025 · 5 min read
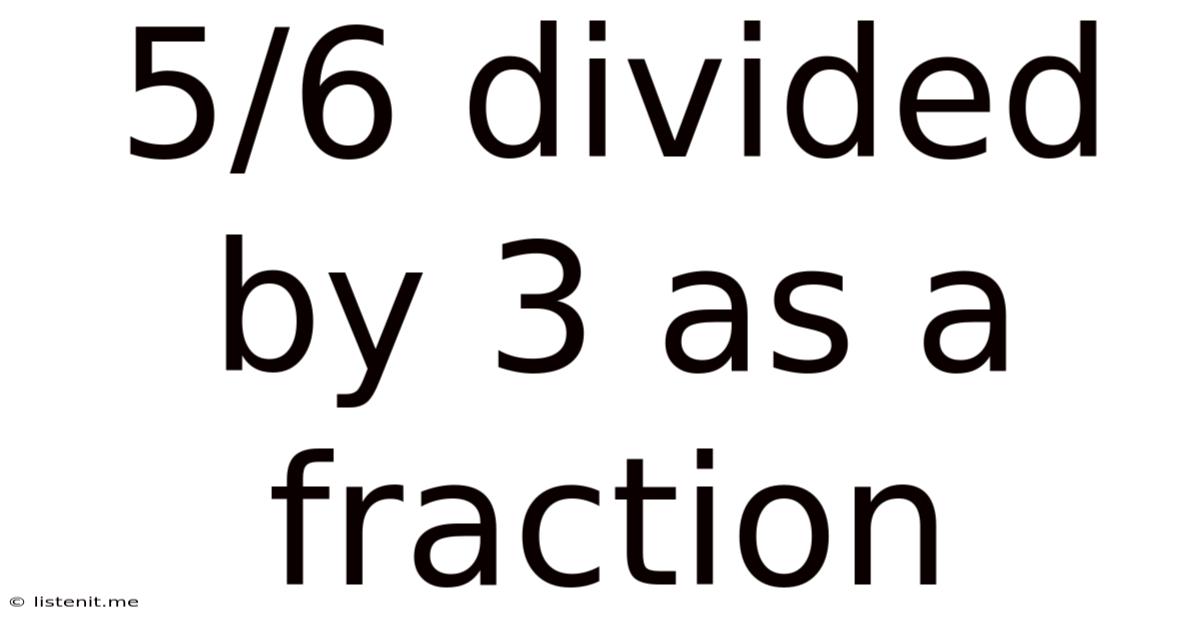
Table of Contents
5/6 Divided by 3: A Deep Dive into Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will explore the division of the fraction 5/6 by the whole number 3, providing a step-by-step solution, exploring the concept's theoretical underpinnings, and offering practical applications to solidify your understanding. We'll even delve into potential real-world scenarios where this type of calculation might be useful. By the end, you'll be confident in tackling similar fraction division problems.
Understanding Fraction Division
Before we tackle 5/6 divided by 3, let's establish a foundational understanding of fraction division. The core concept revolves around finding out "how many times" one fraction goes into another. This is fundamentally different from fraction multiplication. When we multiply fractions, we're finding a part of a part. When we divide fractions, we're finding how many parts of a certain size fit into another.
Key Concept: Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 3 is 1/3.
Solving 5/6 Divided by 3
Now, let's apply this knowledge to our specific problem: 5/6 ÷ 3.
Step 1: Find the reciprocal of the divisor.
Our divisor is 3, which can be written as the fraction 3/1. The reciprocal of 3/1 is 1/3.
Step 2: Change the division to multiplication.
Instead of dividing 5/6 by 3, we'll now multiply 5/6 by the reciprocal of 3, which is 1/3. Our problem now looks like this:
(5/6) * (1/3)
Step 3: Multiply the numerators and denominators.
To multiply fractions, we multiply the numerators together and the denominators together:
(5 * 1) / (6 * 3) = 5/18
Therefore, 5/6 divided by 3 is equal to 5/18.
Visualizing the Solution
Imagine you have a pizza cut into 6 equal slices. You have 5 of these slices (5/6 of the pizza). Now, you want to divide your 5 slices equally among 3 people. Each person would receive 5/18 of the original pizza. This visual representation helps to solidify the abstract mathematical concept.
Alternative Approach: Converting to Improper Fractions
While the reciprocal method is generally preferred for its efficiency, you can also solve this problem by converting the whole number into a fraction and then proceeding with the standard fraction division method.
-
Rewrite the whole number as a fraction: The number 3 can be written as 3/1.
-
Perform the division: (5/6) ÷ (3/1). To divide fractions, we multiply the first fraction by the reciprocal of the second fraction: (5/6) x (1/3) = 5/18
Practical Applications: Real-World Scenarios
The seemingly abstract concept of dividing fractions finds applications in various real-world scenarios. Consider these examples:
-
Baking: If a recipe calls for 5/6 of a cup of flour and you want to make only one-third of the recipe, you would need to calculate (5/6) ÷ 3 = 5/18 of a cup of flour.
-
Sewing: If you need 5/6 of a yard of fabric for a project, and you have three times the required amount, you can find out the total amount of fabric by multiplying: (5/6) x 3 = 5/2 = 2 1/2 yards. The division can be used to determine how many projects you can make from the available fabric.
-
Construction: Imagine you need to divide a length of 5/6 of a meter into 3 equal sections. Each section would be 5/18 of a meter long.
-
Sharing Resources: If 5/6 of a resource needs to be shared equally among 3 individuals, each receives 5/18 of the resource.
Expanding the Concept: Dividing by Fractions
The principles discussed above extend to situations where you're dividing a fraction by another fraction. Let's consider a slightly more complex example:
(5/6) ÷ (1/2)
Again, we use the reciprocal method:
(5/6) * (2/1) = 10/6 = 5/3 = 1 2/3
The process remains the same: find the reciprocal of the second fraction (divisor) and multiply it with the first fraction (dividend).
Troubleshooting Common Mistakes
-
Forgetting the reciprocal: The most common mistake is to simply multiply the fractions without finding the reciprocal of the divisor. Remember, division is the inverse operation of multiplication, necessitating the use of the reciprocal.
-
Incorrect multiplication: Double-check your multiplication of numerators and denominators to avoid simple calculation errors.
-
Not simplifying the fraction: Always simplify your final answer to its lowest terms. In the example of 10/6, we simplified it to 5/3. This makes the answer easier to understand and use.
Mastering Fraction Division: Tips and Practice
Mastering fraction division requires consistent practice and a solid understanding of the underlying concepts. Here are a few tips:
-
Start with simpler examples: Begin by practicing with simpler fractions and whole numbers before moving on to more complex problems.
-
Use visual aids: Use diagrams, pizzas, or other visual aids to visualize the division process. This can make the concept easier to grasp.
-
Practice regularly: Consistent practice is key to mastering any mathematical concept, including fraction division. Work through various examples and problems.
-
Seek assistance when needed: If you're struggling with any aspect of fraction division, don't hesitate to seek help from a teacher, tutor, or online resources.
-
Check your work: Always check your work to ensure accuracy. Use a calculator to verify your results.
Conclusion: A Foundation for Further Mathematical Exploration
Understanding fraction division is a crucial stepping stone in your mathematical journey. It forms the basis for more advanced concepts in algebra, calculus, and other areas of mathematics. By mastering the techniques and concepts presented in this guide, you'll be well-equipped to tackle more complex fraction problems with confidence and accuracy. Remember to practice regularly, and you will build a strong foundation for future mathematical success. The process of dividing 5/6 by 3, although seemingly simple, illustrates fundamental principles that are applicable across a wide range of mathematical problems. Embrace the challenge, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
2 To The Power Of 55
May 25, 2025
-
Greatest Common Factor Of 15 And 24
May 25, 2025
-
1 Hour And 42 Minutes From Now
May 25, 2025
-
Greatest Common Factor Of 20 And 24
May 25, 2025
-
1 2 4 8 16 Sequence Name
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.