10 Is 6 Of What Number
listenit
May 10, 2025 · 4 min read
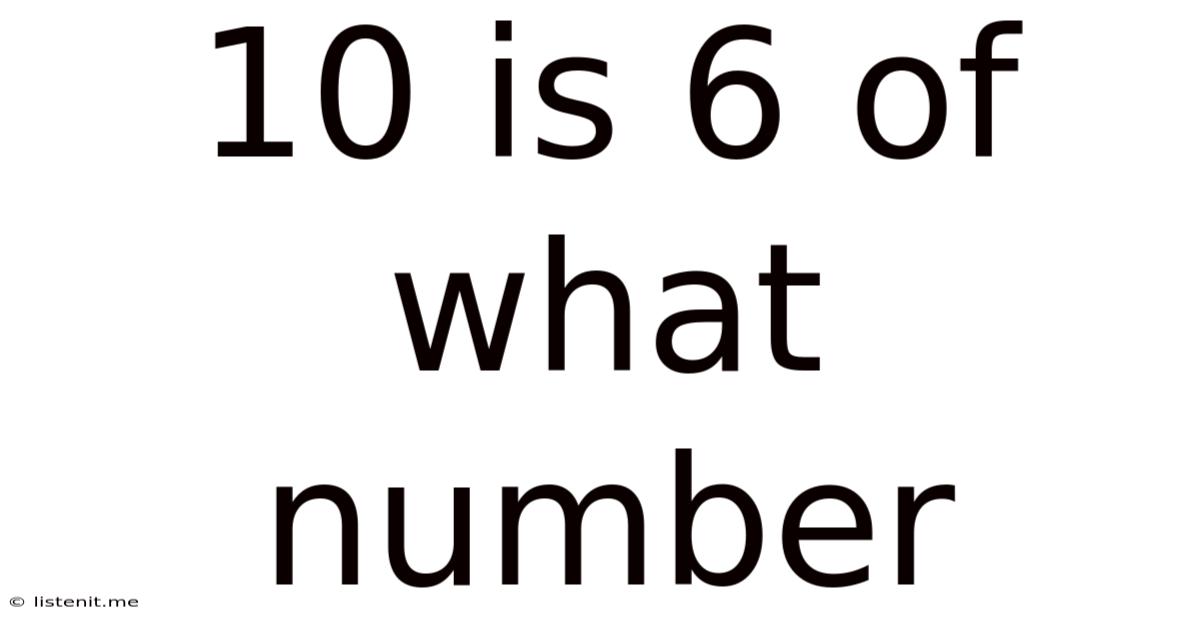
Table of Contents
10 is 60% of What Number? Unraveling the Percentage Puzzle
This seemingly simple question, "10 is 60% of what number?", masks a fundamental concept in mathematics – percentages. Understanding how to solve this type of problem is crucial not only for academic success but also for navigating everyday situations involving discounts, taxes, tips, and more. This article will thoroughly explore the solution, delve into the underlying principles, and provide various methods to tackle similar percentage problems. We'll even look at practical applications and explore how to tackle these calculations quickly and efficiently.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." So, 60% literally means 60 out of 100, or 60/100, which simplifies to 3/5.
This fraction represents a ratio. In our problem, we know that 10 represents 60% (or 3/5) of an unknown number. Our goal is to find that unknown number.
Method 1: Using the Proportion Method
This is arguably the most straightforward method for solving percentage problems. We set up a proportion:
Part/Whole = Percentage/100
In our case:
- Part: 10 (the given value)
- Percentage: 60
- Whole: x (the unknown number we want to find)
Plugging these values into the proportion, we get:
10/x = 60/100
Now, we solve for x using cross-multiplication:
10 * 100 = 60 * x
1000 = 60x
x = 1000/60
x = 16.666... (approximately)
Therefore, 10 is 60% of approximately 16.67.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and setting up an equation. To convert a percentage to a decimal, divide the percentage by 100. So, 60% becomes 0.60 (or simply 0.6).
Our problem can then be expressed as:
0.6 * x = 10
To solve for x, we divide both sides by 0.6:
x = 10 / 0.6
x = 16.666... (approximately)
Again, we arrive at the same answer: 10 is 60% of approximately 16.67.
Method 3: Using the Fraction Method
As mentioned earlier, 60% can be expressed as the fraction 3/5. We can set up an equation using this fraction:
(3/5) * x = 10
To solve for x, we multiply both sides by 5/3 (the reciprocal of 3/5):
x = 10 * (5/3)
x = 50/3
x = 16.666... (approximately)
This method confirms our previous results.
Practical Applications: Real-World Scenarios
Understanding percentage calculations is essential in various real-world situations. Here are a few examples:
- Sales and Discounts: If a store offers a 60% discount on an item, and the discounted price is $10, you can use this method to calculate the original price.
- Taxes and Tips: Calculating the pre-tax amount of a purchase, or determining the amount of tip based on a percentage of a bill.
- Financial Investments: Calculating interest earned on savings accounts or investments. Understanding percentage growth or loss is crucial for financial planning.
- Statistical Analysis: Percentages are fundamental in statistical analysis, used to represent proportions and trends in data.
Advanced Percentage Problems and Variations
The basic percentage problem we've solved can be extended and adapted in numerous ways. Consider these variations:
- Finding the Percentage: Instead of finding the whole, you might be given the whole and the part, and asked to find what percentage the part represents of the whole.
- Finding the Part: You might be given the percentage and the whole, and asked to find the part.
- Multiple Percentage Changes: Imagine a scenario where a price is increased by a certain percentage and then decreased by another percentage. This requires a multi-step calculation.
- Compound Interest: This involves calculating interest not only on the principal but also on accumulated interest from previous periods. This concept introduces exponential growth.
Tips and Tricks for Efficient Calculation
- Master the Basic Methods: Understanding the proportion, decimal, and fraction methods is crucial for tackling any percentage problem.
- Use a Calculator: For complex calculations or those requiring high precision, a calculator is incredibly helpful.
- Practice Regularly: The more you practice solving percentage problems, the faster and more accurately you'll become.
- Check Your Work: Always double-check your calculations to ensure accuracy. A small mistake in a percentage calculation can have significant consequences.
- Break Down Complex Problems: If faced with a more complicated problem, break it down into smaller, more manageable steps.
Conclusion: Mastering the Art of Percentages
Understanding how to solve percentage problems, like "10 is 60% of what number?", is a valuable skill that extends far beyond the classroom. It empowers you to confidently navigate various aspects of daily life, from personal finances to professional endeavors. By mastering the different methods outlined in this article, practicing regularly, and understanding the underlying principles, you can become proficient in solving percentage problems of all complexities and confidently tackle the numerical challenges they present. Remember to always double-check your work and to break down complex problems into simpler, more manageable steps. With enough practice, you'll become adept at solving these problems efficiently and accurately.
Latest Posts
Latest Posts
-
Why Should Chemical Equations Be Balanced
May 10, 2025
-
How Many Moles In 22g Of Co2
May 10, 2025
-
How Do You Know If A Chemical Equation Is Balanced
May 10, 2025
-
Chi Square Test For Homogeneity Vs Independence
May 10, 2025
-
Draw All Stereoisomers Of 1 2 Dichlorocyclohexane
May 10, 2025
Related Post
Thank you for visiting our website which covers about 10 Is 6 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.