10 Divided By 2 1 2
listenit
May 23, 2025 · 5 min read
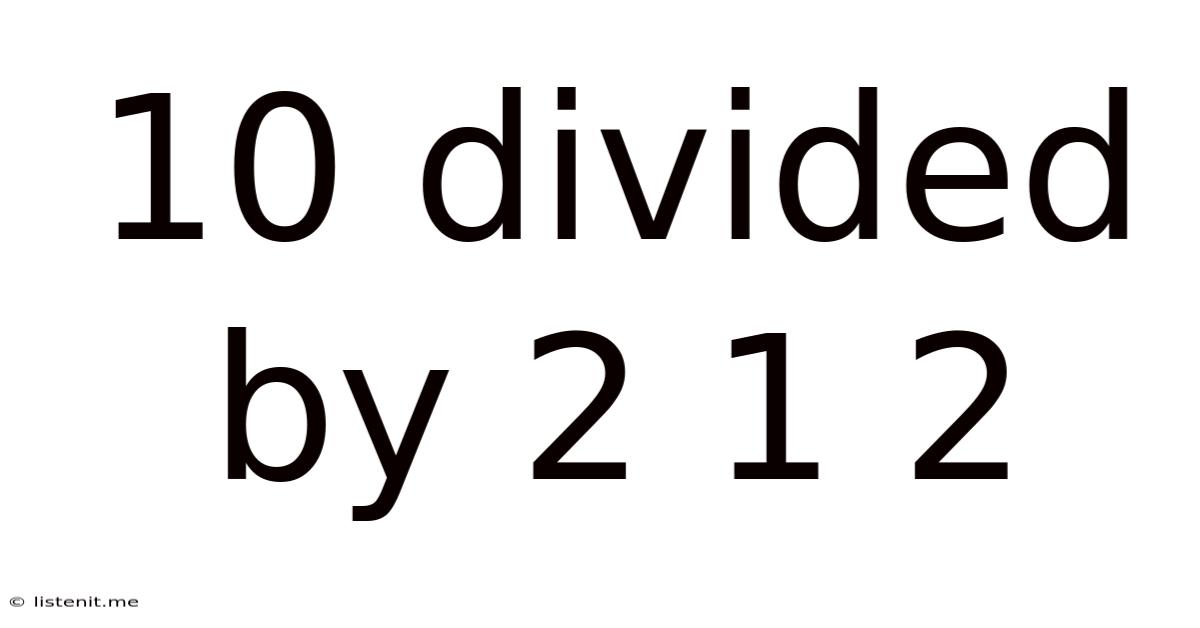
Table of Contents
10 Divided by 2 1/2: A Comprehensive Guide to Fraction Division
Understanding how to divide by fractions is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article delves deep into the process of dividing 10 by 2 1/2, explaining the different methods, their underlying principles, and offering practical examples to solidify your understanding. We will explore why this seemingly simple problem holds significant educational value and how mastering it unlocks a broader understanding of fraction manipulation.
Understanding the Problem: 10 ÷ 2 1/2
The problem, "10 divided by 2 1/2," (or 10 ÷ 2 ½) asks: "How many times does 2 1/2 fit into 10?" This seemingly straightforward question requires a grasp of fraction division, a concept that can be initially challenging for many. The key lies in understanding the relationship between division and multiplication with reciprocals.
Why This Problem Matters
While seemingly simple, this problem serves as an excellent gateway to understanding several crucial mathematical concepts:
- Fraction Division: It reinforces the fundamental process of dividing by fractions, a skill essential for more complex mathematical operations.
- Mixed Numbers: It demonstrates the conversion between mixed numbers (like 2 1/2) and improper fractions, a crucial step in solving fraction division problems.
- Reciprocals: It showcases the use of reciprocals (inverting the fraction) in the process of division, highlighting a fundamental property of fractions.
- Real-World Applications: The ability to solve this problem can be applied to everyday tasks, such as dividing ingredients for a recipe or calculating the number of portions from a given quantity.
Method 1: Converting to Improper Fractions
This is the most common and generally preferred method for dividing fractions. It involves converting the mixed number (2 1/2) into an improper fraction before performing the division.
Step 1: Convert the mixed number to an improper fraction.
To convert 2 1/2 to an improper fraction, we multiply the whole number (2) by the denominator (2), add the numerator (1), and keep the same denominator:
(2 * 2) + 1 = 5
The improper fraction is 5/2.
Step 2: Rewrite the division problem.
Our problem now becomes: 10 ÷ 5/2
Step 3: Invert the second fraction and multiply.
The key to dividing fractions is to invert (flip) the second fraction (the divisor) and multiply:
10 ÷ 5/2 = 10 * 2/5
Step 4: Simplify and solve.
We can now simplify before multiplying:
10 * 2/5 = (10/1) * (2/5) = 20/5 = 4
Therefore, 10 divided by 2 1/2 equals 4.
Method 2: Using Decimal Representation
Another method involves converting both the dividend (10) and the divisor (2 1/2) into decimal numbers.
Step 1: Convert the mixed number to a decimal.
2 1/2 is equivalent to 2.5.
Step 2: Perform the division.
Now, perform the division using decimal numbers:
10 ÷ 2.5 = 4
This method provides a quick and straightforward solution, especially when using a calculator. However, it's crucial to understand the underlying principles of fraction division, which the first method more clearly demonstrates.
Method 3: Repeated Subtraction
While less efficient than the previous methods, especially for larger numbers, repeated subtraction offers a visual and intuitive understanding of division.
This method asks, "How many times can we subtract 2 1/2 from 10 before reaching 0?"
10 - 2.5 = 7.5 7.5 - 2.5 = 5 5 - 2.5 = 2.5 2.5 - 2.5 = 0
We subtracted 2.5 four times to reach 0, therefore, 10 divided by 2 1/2 is 4.
Practical Applications and Real-World Examples
The ability to divide by fractions has numerous real-world applications:
- Cooking and Baking: Dividing ingredients for recipes often involves fractions. If a recipe calls for 2 1/2 cups of flour and you want to halve the recipe, you need to divide the flour quantity by 2.
- Construction and Measurement: Calculating material quantities for construction projects frequently requires working with fractions and decimals. Dividing lengths and areas often involves fraction division.
- Financial Calculations: Dividing shares or calculating portions of investments often involves fractional amounts.
- Data Analysis: Data analysis and statistical calculations frequently use fractions and require proficiency in fraction division.
Troubleshooting Common Mistakes
Common errors when dividing fractions include:
- Incorrectly converting mixed numbers: Ensure you accurately convert mixed numbers to improper fractions before proceeding.
- Forgetting to invert and multiply: Remember the crucial step of inverting the second fraction (divisor) before multiplying.
- Errors in simplification: Always simplify fractions before multiplying to avoid working with large numbers.
- Incorrect decimal conversion: When using the decimal method, ensure accurate decimal conversion of fractions.
Expanding Your Knowledge: Beyond 10 ÷ 2 1/2
Mastering this fundamental concept opens doors to more advanced fraction operations. Here are some areas to explore further:
- Dividing larger numbers by fractions: Apply the same methods to solve problems involving larger dividends and more complex fractions.
- Dividing fractions by fractions: Practice dividing any fraction by another fraction, using the same principles of inverting and multiplying.
- Complex fraction division: Tackle problems involving complex fractions (fractions within fractions).
Conclusion: Mastering Fraction Division
The seemingly simple problem of 10 divided by 2 1/2 provides a robust foundation for understanding fraction division. By mastering this concept using the various methods explained here, you build a strong base for tackling more complex mathematical challenges and applying these skills to real-world situations. Remember, consistent practice and understanding the underlying principles are crucial to mastering fraction division and becoming proficient in mathematics. Through repeated practice and exploring more complex problems, you can develop a confident and fluent understanding of fraction manipulation.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 6 And 27
May 24, 2025
-
2 Is What Percent Of 24
May 24, 2025
-
What Is 15 Percent Of 100000
May 24, 2025
-
What Is 20 Off Of 6
May 24, 2025
-
What Is 3 4 Divided By 1 2
May 24, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.