1 In 10000 As A Percentage
listenit
May 23, 2025 · 5 min read
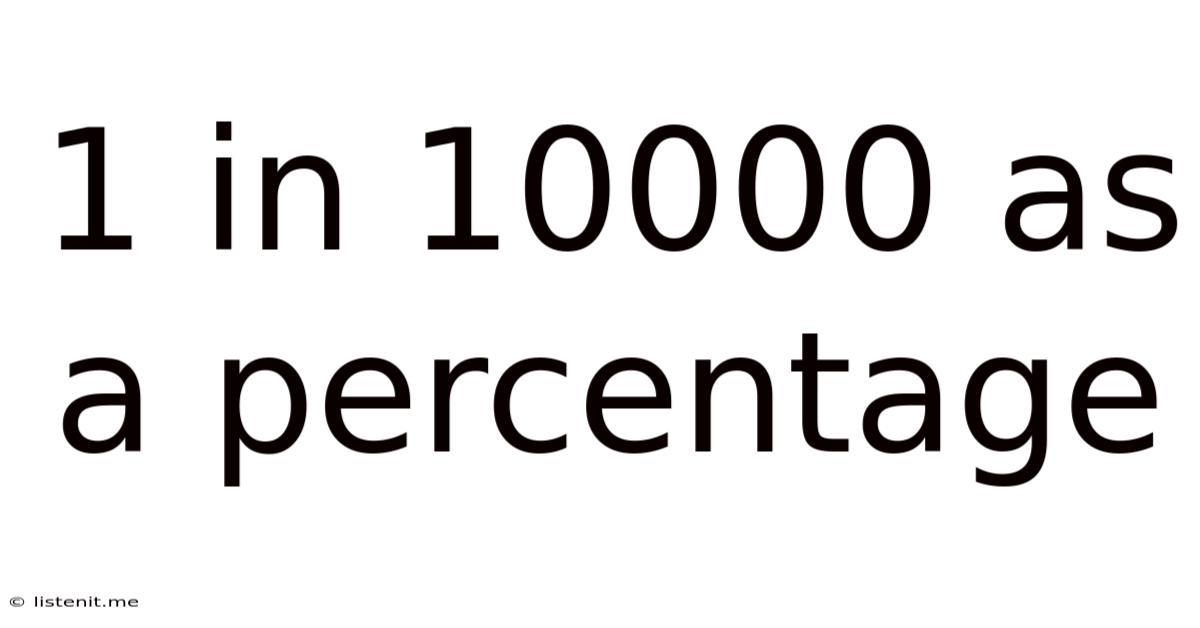
Table of Contents
1 in 10,000 as a Percentage: Understanding Rarity and Probability
Understanding probabilities and expressing them in different formats is crucial in various fields, from data analysis and statistics to risk assessment and everyday decision-making. Often, we encounter probabilities expressed as ratios (like "1 in 10,000") that need to be converted into percentages for better comprehension and comparison. This article delves into how to convert the ratio "1 in 10,000" into a percentage, explores its implications, and provides practical examples across diverse contexts.
Converting 1 in 10,000 to a Percentage
The core concept behind this conversion is simple: a percentage represents a fraction of 100. To convert a ratio like "1 in 10,000" to a percentage, we need to express the ratio as a fraction and then multiply it by 100.
Here's the step-by-step process:
-
Express the ratio as a fraction: "1 in 10,000" can be written as the fraction 1/10,000.
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (10,000): 1 ÷ 10,000 = 0.0001
-
Multiply the decimal by 100: 0.0001 x 100 = 0.01%
Therefore, 1 in 10,000 is equal to 0.01%.
Understanding the Significance of 0.01%
A probability of 0.01% signifies a very low likelihood of an event occurring. This means that for every 10,000 instances, you'd expect the event to happen only once. This rarity has significant implications depending on the context.
Low Probability Events and Risk Assessment
In risk assessment, a 0.01% probability might be considered negligible for some applications but critically important for others. Consider these examples:
-
Medical procedures: A 0.01% risk of a serious complication during surgery might be acceptable if the benefits significantly outweigh the risk. However, even this low probability warrants thorough discussion with the patient.
-
Engineering and manufacturing: In the production of critical components for aircraft or medical devices, a 0.01% failure rate might be deemed unacceptable and necessitate stringent quality control measures. The consequences of failure are too high to tolerate even a small probability.
-
Financial investments: While a 0.01% chance of a significant financial loss might seem small, the potential magnitude of that loss could make it a relevant factor in investment decisions, particularly for large sums of money.
Rare Events and Statistical Significance
In statistical analysis, a 0.01% probability often falls well below the threshold for statistical significance. Researchers typically use p-values to determine the likelihood of observing results if there is no actual effect. A p-value below 0.05 (or 5%) is often considered statistically significant, meaning that the results are unlikely due to chance alone. A 0.01% probability (0.0001) is far below this threshold, strongly suggesting a real effect.
Practical Applications Across Different Fields
The application of understanding "1 in 10,000" as 0.01% extends far beyond theoretical probability calculations. Let's examine specific examples:
Genetics and Disease Risk
Some genetic mutations might have a probability of occurrence as low as 1 in 10,000. Genetic counselors use this information to assess the risk of inheriting specific diseases or conditions within families. Even though the probability is low, understanding this probability helps in providing informed choices about family planning and preventative measures.
Lottery Probabilities
Lottery wins are classic examples of low-probability events. The odds of winning a major lottery jackpot are often far lower than 1 in 10,000. Understanding these probabilities helps in managing expectations and making rational decisions about gambling.
Natural Disasters and Risk Prediction
Predicting the probability of rare natural disasters, such as large-scale volcanic eruptions or meteor impacts, involves analyzing historical data and constructing probabilistic models. Even though the probability of a specific event might be as low as 0.01% in a given year, the potential catastrophic consequences necessitate preparedness and mitigation strategies.
Quality Control and Manufacturing
In manufacturing, quality control processes aim to minimize the probability of defects. A 0.01% defect rate might be a target for high-precision manufacturing processes, although achieving such low rates requires meticulous attention to detail and sophisticated quality control techniques.
Cybersecurity and Data Breaches
In the realm of cybersecurity, a 0.01% probability of a successful data breach might seem insignificant, but the potential consequences – financial losses, reputational damage, and legal repercussions – are substantial enough to warrant robust security measures.
Comparing Probabilities: Putting 0.01% in Context
To truly grasp the significance of 0.01%, it's helpful to compare it to other probabilities:
- 1% (1 in 100): A relatively common event.
- 0.1% (1 in 1000): An uncommon event.
- 0.01% (1 in 10,000): A very rare event.
- 0.001% (1 in 100,000): An extremely rare event.
By comparing 0.01% to these other probabilities, we can better understand its position within the spectrum of likelihood. The further you move toward 0%, the rarer the event becomes.
Beyond the Numbers: The Importance of Context
While the numerical value of 0.01% is important, understanding the context is crucial. The significance of a 0.01% probability depends heavily on the potential consequences of the event. A 0.01% chance of winning a million dollars is very different from a 0.01% chance of a catastrophic plane crash.
Conclusion: From Ratio to Understanding
Converting "1 in 10,000" to 0.01% provides a clearer and more easily comparable measure of probability. Understanding this low probability and its implications is crucial in various fields, from risk assessment and statistical analysis to decision-making in diverse contexts. Remember that while the number is small, the context and potential consequences are what truly determine its significance. By understanding both the numerical value and the context, we can make informed decisions and manage risks effectively.
Latest Posts
Latest Posts
-
What Is The Gcf Of 100 And 30
May 24, 2025
-
What Is 1 8 Of 32
May 24, 2025
-
4 Is What Percent Of 18
May 24, 2025
-
How To Calculate Annual Salary From Biweekly
May 24, 2025
-
1975 To 2023 How Many Years
May 24, 2025
Related Post
Thank you for visiting our website which covers about 1 In 10000 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.