4 Is What Percent Of 18
listenit
May 24, 2025 · 5 min read
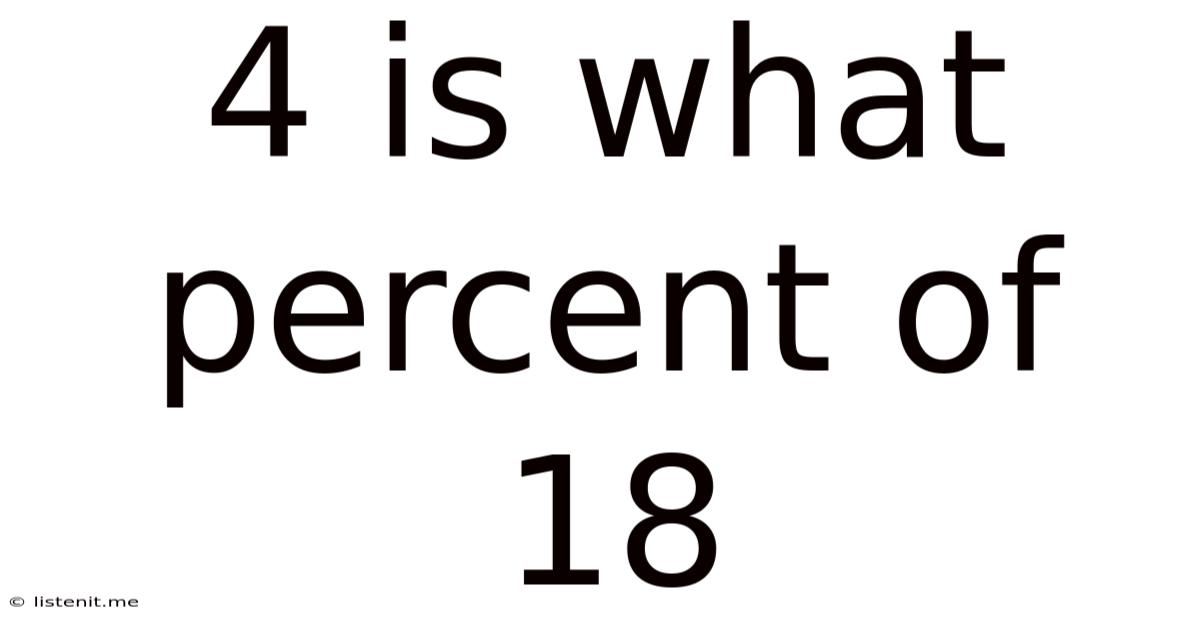
Table of Contents
4 is What Percent of 18? A Deep Dive into Percentage Calculations
This seemingly simple question, "4 is what percent of 18?", opens the door to a world of practical applications and fundamental mathematical concepts. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to comprehending statistics and financial data. This article will not only answer the question directly but also explore the underlying principles, providing you with the tools to solve similar percentage problems independently. We will cover multiple methods of calculation, discuss real-world examples, and explore the broader context of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." When we say "x percent," we are essentially saying "x out of 100" or x/100. This representation is crucial for understanding how percentages work.
Method 1: Using the Percentage Formula
The most direct way to solve "4 is what percent of 18?" is to use the standard percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 4 (the smaller amount)
- Whole: 18 (the larger amount)
Plugging these values into the formula:
(4 / 18) * 100 = Percentage
Calculating this:
(0.2222...) * 100 ≈ 22.22%
Therefore, 4 is approximately 22.22% of 18. The "..." indicates that the decimal continues infinitely. For practical purposes, rounding to two decimal places is generally sufficient.
Method 2: Proportion Method
Another effective method involves setting up a proportion. We can express the problem as a ratio:
4/18 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
4 * 100 = 18 * x
400 = 18x
x = 400 / 18
x ≈ 22.22%
This method reinforces the concept of equivalent ratios and provides an alternative approach to solving percentage problems.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100.
First, express the relationship as a fraction: 4/18
Then, convert the fraction to a decimal by performing the division: 4 ÷ 18 ≈ 0.2222
Finally, multiply the decimal by 100 to obtain the percentage: 0.2222 * 100 ≈ 22.22%
This method highlights the direct relationship between decimals and percentages.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations is vital in numerous real-life scenarios:
-
Retail Discounts: A store offers a 20% discount on an item priced at $50. The discount amount is calculated as (20/100) * $50 = $10. The final price is $50 - $10 = $40. This same principle applies to sales tax calculations, where the tax amount is a percentage of the purchase price.
-
Financial Calculations: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions. For instance, a 5% annual interest on a $1000 investment will yield $50 in interest after one year.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions and trends in data. For example, a survey might reveal that 60% of respondents prefer a particular product. This percentage helps summarize the results and draw conclusions.
-
Grade Calculations: Academic grades are often expressed as percentages, representing the ratio of points earned to total possible points. A score of 85 out of 100 translates to an 85% grade.
-
Tip Calculations: Restaurants often suggest tipping a certain percentage of the bill (e.g., 15% or 20%). Calculating the tip amount based on the percentage helps determine the total cost.
-
Commission Calculations: Sales representatives often earn a commission, which is a percentage of their sales. Calculating the commission earned based on sales figures is essential for determining income.
Expanding the Concept: Solving for Different Variables
The fundamental formula (Part / Whole) * 100 = Percentage can be rearranged to solve for different variables:
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example: What is 25% of 60? The formula becomes: (25/100) * 60 = Part.
-
Finding the Whole: If you know the percentage and the part, you can find the whole. For example: 10 is 20% of what number? The formula becomes: (10 / (20/100)) = Whole.
Mastering these variations allows for a broader application of percentage calculations.
Beyond the Basics: Advanced Percentage Concepts
While the basic percentage formula is sufficient for many scenarios, more advanced concepts include:
-
Percentage Change: This involves calculating the increase or decrease in a value relative to its original value. The formula is: [(New Value - Old Value) / Old Value] * 100.
-
Compound Interest: This refers to interest earned not only on the principal amount but also on accumulated interest. It's a crucial concept in finance and investment.
-
Percentage Points: It's important to distinguish between percentage change and percentage points. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original 20%.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "4 is what percent of 18?", unlocks a world of practical applications and mathematical skills. By understanding the fundamental formula, different calculation methods, and real-world applications, you equip yourself with a valuable tool for navigating various aspects of life, from personal finance to professional endeavors. Mastering percentages is not just about solving mathematical problems; it's about developing a crucial skill for effective decision-making and data analysis in a world increasingly reliant on numerical information. Remember to practice regularly and explore diverse problem-solving approaches to build confidence and mastery in percentage calculations. This will serve you well in various academic, professional, and personal situations. The ability to quickly and accurately calculate percentages is a valuable asset in many walks of life.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 24 And 60
May 24, 2025
-
What Is 4 Percent Of 2000
May 24, 2025
-
How Many Years From 1987 To 2024
May 24, 2025
-
1 4 Divided By 6 As A Fraction
May 24, 2025
-
What Is 35 Percent Of 40
May 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.