1/6 Divided By 2 In Fraction
listenit
May 23, 2025 · 5 min read
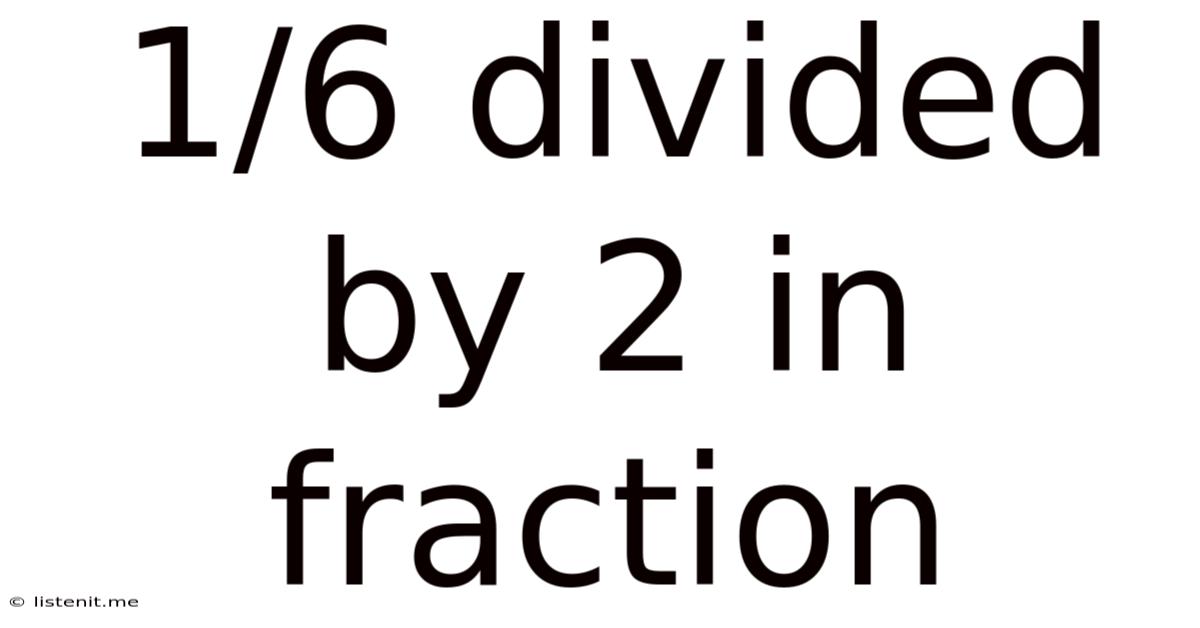
Table of Contents
1/6 Divided by 2: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with widespread applications. This comprehensive guide will walk you through the process of dividing fractions, specifically addressing the problem of 1/6 divided by 2, and will equip you with the knowledge and skills to tackle similar problems with confidence. We'll explore various methods, provide practical examples, and delve into the underlying principles to ensure a thorough understanding.
Understanding Fraction Division
Before diving into the specifics of 1/6 divided by 2, let's establish a solid foundation in fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by simply swapping the numerator and the denominator.
Key Concept: Dividing by a fraction is equivalent to multiplying by its reciprocal.
For example, dividing by 1/2 is the same as multiplying by 2/1 (or simply 2). This fundamental principle simplifies the process considerably.
Solving 1/6 Divided by 2
Now, let's tackle the problem at hand: 1/6 divided by 2.
Following the rule above, we can rewrite the problem as:
1/6 ÷ 2 = 1/6 × 1/2
Notice how we've changed the division operation into a multiplication operation by using the reciprocal of 2, which is 1/2. Now, we simply multiply the numerators together and the denominators together:
(1 × 1) / (6 × 2) = 1/12
Therefore, 1/6 divided by 2 equals 1/12.
Alternative Methods for Solving Fraction Division Problems
While the reciprocal method is the most straightforward approach, there are alternative ways to solve fraction division problems. Let's explore a few:
Method 1: Using a Common Denominator
This method involves converting the whole number (in this case, 2) into a fraction with a common denominator.
-
Convert the whole number to a fraction: 2 can be written as 2/1.
-
Find a common denominator: The common denominator for 1/6 and 2/1 is 6.
-
Rewrite the fractions: 2/1 becomes 12/6 (by multiplying both the numerator and denominator by 6).
-
Perform the division: Now we have (1/6) ÷ (12/6). When dividing fractions with the same denominator, you can simply divide the numerators: 1 ÷ 12 = 1/12.
Therefore, using the common denominator method also gives us the answer 1/12.
Method 2: Visual Representation
While less efficient for complex problems, visualizing the problem can be helpful, particularly for beginners. Imagine you have a pizza cut into six slices. You have one slice (1/6). If you want to divide this slice into two equal parts, each part would represent 1/12 of the whole pizza.
Practical Applications of Fraction Division
Understanding fraction division isn't just an academic exercise. It has numerous real-world applications, including:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafting: Cutting fabric or other materials accurately often involves fractions.
- Construction and Engineering: Precise measurements are crucial, and fractions are often involved.
- Data Analysis: Working with proportions and percentages often necessitates fraction division.
Expanding on Fraction Division: More Complex Examples
Let's consider more challenging problems to solidify your understanding:
Example 1: 3/4 divided by 1/2
- Find the reciprocal of 1/2: 2/1
- Multiply: (3/4) × (2/1) = 6/4
- Simplify: 6/4 = 3/2 or 1 1/2
Example 2: 2 1/3 divided by 1/6
- Convert the mixed number to an improper fraction: 2 1/3 = 7/3
- Find the reciprocal of 1/6: 6/1
- Multiply: (7/3) × (6/1) = 42/3
- Simplify: 42/3 = 14
Example 3: 1/8 divided by 3/4
- Find the reciprocal of 3/4: 4/3
- Multiply: (1/8) × (4/3) = 4/24
- Simplify: 4/24 = 1/6
Troubleshooting Common Mistakes in Fraction Division
Several common mistakes can hinder your ability to solve fraction division problems accurately. Let's address some of these:
-
Forgetting to use the reciprocal: This is the most common mistake. Remember, you must use the reciprocal of the divisor (the number you're dividing by).
-
Incorrect simplification: Always simplify your fractions to their lowest terms.
-
Confusing multiplication with division: Keep the distinction clear between multiplication and division of fractions.
-
Improperly converting mixed numbers: Make sure you correctly convert mixed numbers into improper fractions before performing the division.
Mastering Fraction Division: Tips and Practice
Mastering any mathematical concept requires practice. Here are some tips to help you improve your skills in fraction division:
-
Start with simple problems: Gradually increase the complexity of the problems you attempt.
-
Use different methods: Try solving the same problem using multiple methods to reinforce your understanding.
-
Check your work: Always verify your answer using a calculator or alternative methods.
-
Seek help when needed: Don't hesitate to ask for assistance if you're struggling.
By consistently practicing and applying these strategies, you'll build a solid foundation in fraction division and confidently tackle even the most challenging problems. Remember the core principle: dividing by a fraction is the same as multiplying by its reciprocal. With consistent effort and practice, mastering fraction division will become second nature. Understanding this fundamental concept opens doors to more advanced mathematical concepts and strengthens your overall problem-solving skills.
Latest Posts
Latest Posts
-
What Is The Prime Factorization For 23
May 24, 2025
-
What Is 5 Divided By 20
May 24, 2025
-
How Many Days In A 3 Months
May 24, 2025
-
What Is The Gcf Of 8 And 52
May 24, 2025
-
What Is 4 Percent Of 3000
May 24, 2025
Related Post
Thank you for visiting our website which covers about 1/6 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.