What Is 5 Divided By 20
listenit
May 24, 2025 · 5 min read
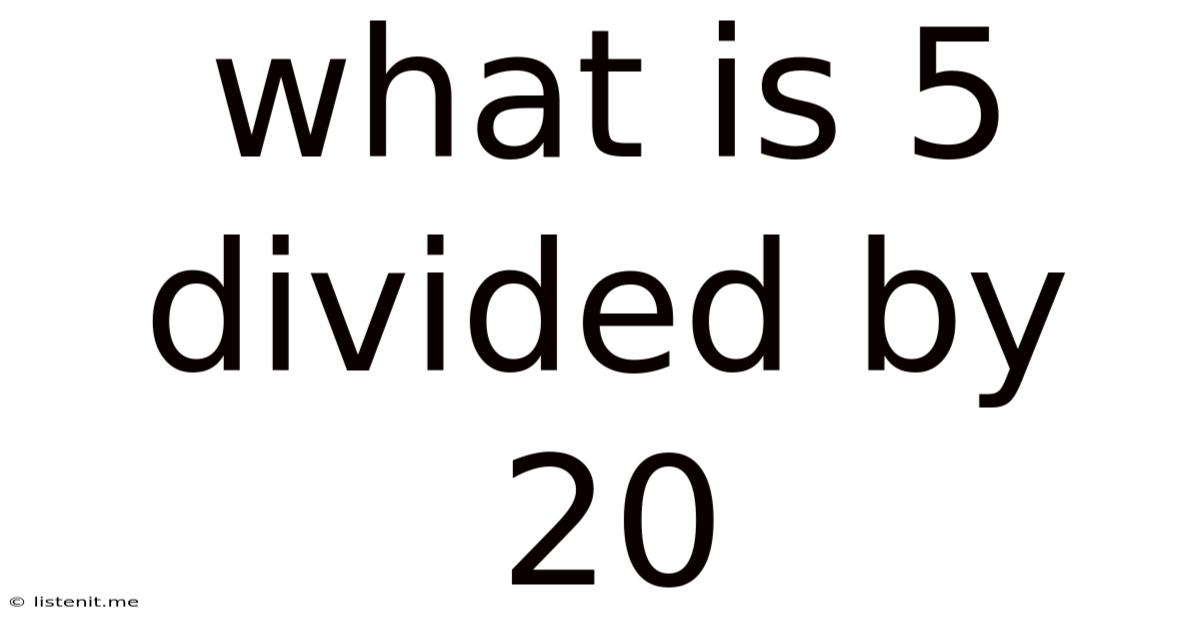
Table of Contents
What is 5 Divided by 20? A Deep Dive into Division and its Applications
The seemingly simple question, "What is 5 divided by 20?" opens a door to a world of mathematical concepts, practical applications, and problem-solving strategies. While the answer itself is straightforward, understanding the underlying principles and exploring its broader context enriches our mathematical understanding and enhances our ability to tackle more complex problems. This article will delve deep into this seemingly simple division problem, exploring its solution, its implications, and its relevance in various fields.
Understanding Division: The Basics
Before diving into the specifics of 5 divided by 20, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. We can represent division in several ways:
- Using the division symbol (÷): 5 ÷ 20
- Using a fraction: 5/20
- Using the division symbol (/): 5/20
In essence, the question "What is 5 divided by 20?" asks: "If we have 5 units and we want to divide them into 20 equal parts, how large is each part?"
Calculating 5 Divided by 20
The calculation is straightforward:
5 ÷ 20 = 0.25
This means that if you divide 5 into 20 equal parts, each part will be 0.25 or one-quarter (1/4). This can also be expressed as 25%. Understanding this simple calculation lays the foundation for grasping more intricate mathematical concepts.
Different Perspectives on Division: Fractions and Decimals
The result of 5 divided by 20, 0.25, can be represented in multiple ways, highlighting the interconnectedness of mathematical concepts.
Fractions: A Visual Representation
The fraction 5/20 represents the division problem visually. It signifies 5 parts out of a total of 20 parts. This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (5) and the denominator (20), which is 5. Dividing both the numerator and the denominator by 5, we get:
5 ÷ 5 / 20 ÷ 5 = 1/4
This simplification shows that 5/20 is equivalent to 1/4, further illustrating the size of each part when 5 is divided into 20 equal portions.
Decimals: A Numerical Representation
The decimal representation, 0.25, provides a precise numerical value for the result. Decimals are particularly useful in practical applications where precise measurements or calculations are required, such as in engineering, finance, or scientific research. The decimal 0.25 clearly indicates that each part is a quarter of a unit.
Percentages: Expressing Proportions
Expressing the result as a percentage, 25%, provides a clear indication of the proportional relationship between the divided quantity (5) and the total quantity (20). This representation is commonly used to express ratios and proportions, making it easily understandable in various contexts.
Real-World Applications of Division: Beyond the Classroom
The seemingly simple division problem of 5 divided by 20 finds applications in numerous real-world scenarios. Understanding this basic calculation is crucial for navigating everyday situations and tackling more complex problems.
Sharing Resources
Imagine you have 5 pizzas to share equally among 20 people. The calculation 5 ÷ 20 = 0.25 tells us each person will receive 0.25 or one-quarter of a pizza.
Calculating Proportions
Suppose a recipe calls for 20 cups of flour and you only have 5 cups. To determine the proportional amount of other ingredients, you need to divide 5 by 20 to find the scaling factor (0.25). This allows you to adjust the recipe proportionally, maintaining the correct flavor balance.
Calculating Percentages
If you scored 5 points out of a possible 20 points on a quiz, you can calculate your percentage score by dividing 5 by 20 and multiplying by 100: (5/20) * 100 = 25%. This shows you achieved 25% on the quiz.
Financial Calculations
Understanding division is fundamental in financial calculations. For example, if you invest $5 and it generates a profit of $20, you can calculate the return on investment by dividing the profit ($20) by the investment ($5). This illustrates the importance of division in evaluating financial returns.
Expanding the Concept: Division with Larger Numbers and Different Types of Numbers
The principle of division remains consistent even with larger numbers or different types of numbers. Let's consider some examples:
Division with Larger Numbers
Imagine dividing 500 by 2000. The process is the same, resulting in 0.25, demonstrating the scalability of the division principle. The result remains consistent irrespective of the magnitude of the numbers, highlighting the underlying mathematical concept.
Division with Fractions
Dividing fractions involves a slightly different approach but the core principle remains the same. For example, dividing 5/8 by 20/16 requires multiplying the first fraction by the reciprocal of the second. This results in a numerical value that represents the equal division of the fractions, showing how division extends to fractional values.
Division with Negative Numbers
Dividing a positive number by a negative number, or vice versa, introduces the concept of signs in division. The rule remains straightforward: a positive number divided by a negative number gives a negative result, and vice versa.
Error Handling and Division by Zero
One critical aspect of division is understanding the concept of division by zero. Division by zero is undefined in mathematics. It's crucial to understand that you cannot divide any number by zero because it results in an undefined answer. This is a fundamental concept in mathematics and a common error to avoid.
Conclusion: The Significance of Understanding Division
The seemingly simple problem, "What is 5 divided by 20?" offers a gateway to exploring the vast world of mathematics and its practical applications. From understanding basic arithmetic operations to tackling more complex mathematical problems, mastering division is fundamental. Its applications extend beyond the classroom, touching various aspects of our daily lives, from sharing resources and calculating proportions to making financial decisions. Understanding the nuances of division, including different representations (fractions, decimals, percentages), and error handling (division by zero) is crucial for developing a strong mathematical foundation and enhancing problem-solving skills. This knowledge empowers us to confidently approach more challenging mathematical concepts and successfully navigate the complexities of the real world.
Latest Posts
Latest Posts
-
How Many Months Is 26 Years
May 24, 2025
-
What Is 20 Percent Of 5 Dollars
May 24, 2025
-
August 19 Day Of The Week
May 24, 2025
-
1 1 2 1 1 4
May 24, 2025
-
How Many Days Since August 5th
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Divided By 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.