1.5 Of The Number Is 60
listenit
May 25, 2025 · 4 min read
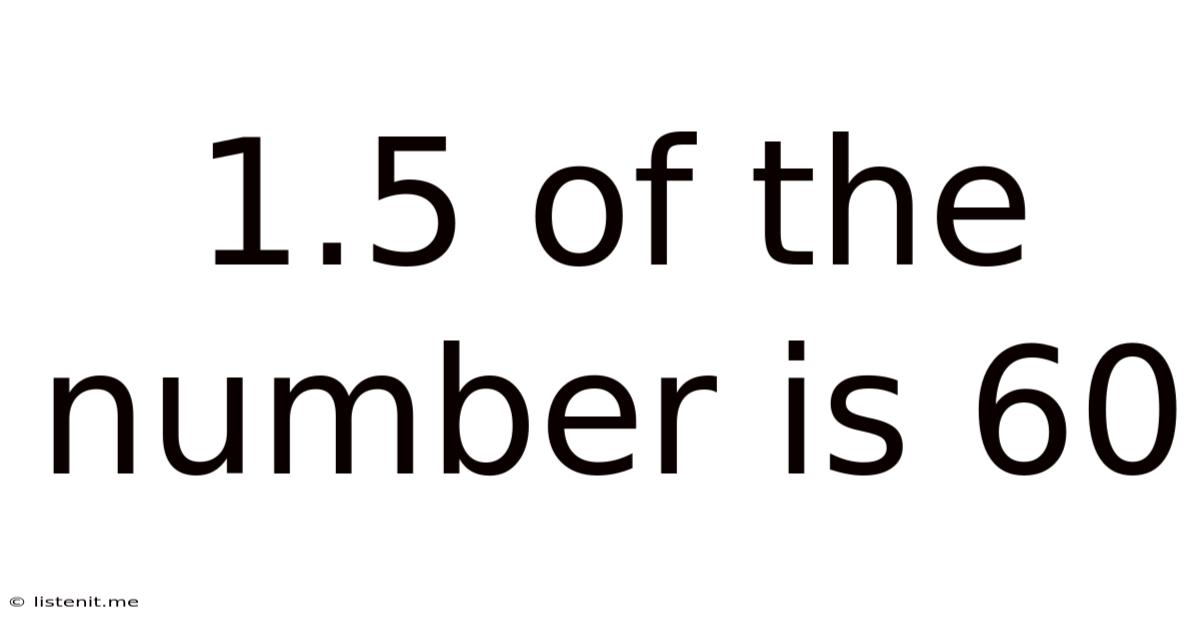
Table of Contents
Unraveling the Mystery: 1.5 of a Number is 60
This seemingly simple mathematical statement, "1.5 of a number is 60," opens a door to a world of problem-solving strategies and a deeper understanding of fundamental mathematical concepts. While the solution might seem straightforward to some, exploring this problem allows us to delve into various approaches, strengthening our mathematical intuition and developing crucial problem-solving skills applicable far beyond this specific equation.
This article will comprehensively explore the solution to this problem, examining different methods, highlighting the underlying mathematical principles, and even extending the concept to more complex scenarios. We'll focus on clear explanations, step-by-step guides, and practical applications, making the learning process engaging and rewarding.
Understanding the Problem: Deconstructing "1.5 of a Number is 60"
Before diving into solutions, let's dissect the problem statement itself. The phrase "1.5 of a number" signifies 1.5 times that number. In mathematical terms, we can represent this as 1.5 * x = 60, where 'x' represents the unknown number. Understanding this translation from words to an algebraic equation is the crucial first step in solving any mathematical word problem.
This seemingly simple equation holds the key to unlocking more complex problems. Understanding the relationship between the multiplier (1.5), the unknown variable (x), and the product (60) forms the foundation for understanding proportional relationships, percentages, and more advanced algebraic concepts.
Method 1: Solving the Equation Directly
The most straightforward approach to solving the equation 1.5 * x = 60 is to isolate the variable 'x'. We can achieve this by dividing both sides of the equation by 1.5:
x = 60 / 1.5
To simplify this division, we can convert 1.5 into a fraction: 1.5 = 3/2. Therefore, the equation becomes:
x = 60 / (3/2)
Reciprocating the fraction and multiplying gives:
x = 60 * (2/3)
x = 120 / 3
x = 40
Therefore, the number is 40. This method directly applies algebraic manipulation to solve for the unknown variable, a fundamental skill in mathematics.
Method 2: Using Proportions
Another effective approach involves setting up a proportion. We know that 1.5 is to 60 as 1 is to x. We can represent this proportion as:
1.5 / 60 = 1 / x
Cross-multiplying gives:
1.5 * x = 60
This equation is identical to the one we derived in Method 1, leading to the same solution: x = 40. This method highlights the relationship between ratios and proportions, demonstrating that different approaches can lead to the same result.
Method 3: Applying Percentage Concepts
We can also approach this problem using percentage concepts. 1.5 can be interpreted as 150% (1.5 * 100%). The problem can be rephrased as: "150% of a number is 60." To find the number, we can use the formula:
Number = (Percentage / 100) * Value
In this case, Percentage = 150, and Value = 60. Therefore:
Number = (150 / 100) * 60
Number = 1.5 * 60
Number = 90
Wait a minute! This result (90) is different from the previous results (40). This discrepancy highlights a crucial point: the phrasing "1.5 of a number" is ambiguous. While it often implies multiplication, it's essential to be precise in mathematical language. In this context, "1.5 of a number" should be interpreted as 1.5 * x = 60, as we solved earlier. The percentage method requires a clearer specification of the percentage in relation to the whole number. If the question intended to say 150% OF a number, then the calculation will lead to 90.
Extending the Concept: More Complex Scenarios
Let's extend this problem-solving approach to more challenging scenarios. Consider this:
Problem: 2.75 of a number is 110. What is the number?
Using the same principle, we can set up the equation:
2.75 * x = 110
Dividing both sides by 2.75:
x = 110 / 2.75
x = 40
This demonstrates that the fundamental approach remains consistent, regardless of the specific numbers involved. The key is to translate the word problem into an algebraic equation and then solve for the unknown variable.
Real-World Applications
This seemingly simple problem has significant real-world applications. Imagine calculating discounts, figuring out ingredient quantities in recipes (scaling recipes up or down), or determining the cost of items with fractional pricing. Understanding how to solve for an unknown variable using these methods is essential in many professional fields, including finance, engineering, and even cooking.
Conclusion: Mastering Mathematical Problem-Solving
The problem, "1.5 of a number is 60," serves as a fantastic gateway to honing problem-solving skills. By exploring various solution methods, we've not only found the answer (40) but also strengthened our understanding of algebraic manipulation, proportions, and the importance of precise mathematical language. Remember, the ability to translate real-world problems into mathematical equations is a valuable skill that extends far beyond the classroom and into many aspects of life. The key to successfully tackling more complex mathematical problems lies in breaking them down into smaller, manageable steps, identifying the underlying principles, and applying appropriate strategies. The ability to choose between multiple methods illustrates that flexibility and understanding of fundamental mathematical principles greatly improve your analytical ability. Practice consistently and soon you’ll find solving these problems as straightforward as 1, 2, 3!
Latest Posts
Latest Posts
-
30 Days After November 25 2024
May 25, 2025
-
18 Out Of 35 As A Percentage
May 25, 2025
-
12am To 5am Is How Many Hours
May 25, 2025
-
5 Divided By 4 As A Fraction
May 25, 2025
-
How To Calculate Volume Of A Room
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1.5 Of The Number Is 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.