1 3 Of 1 2 Cup
listenit
May 10, 2025 · 4 min read
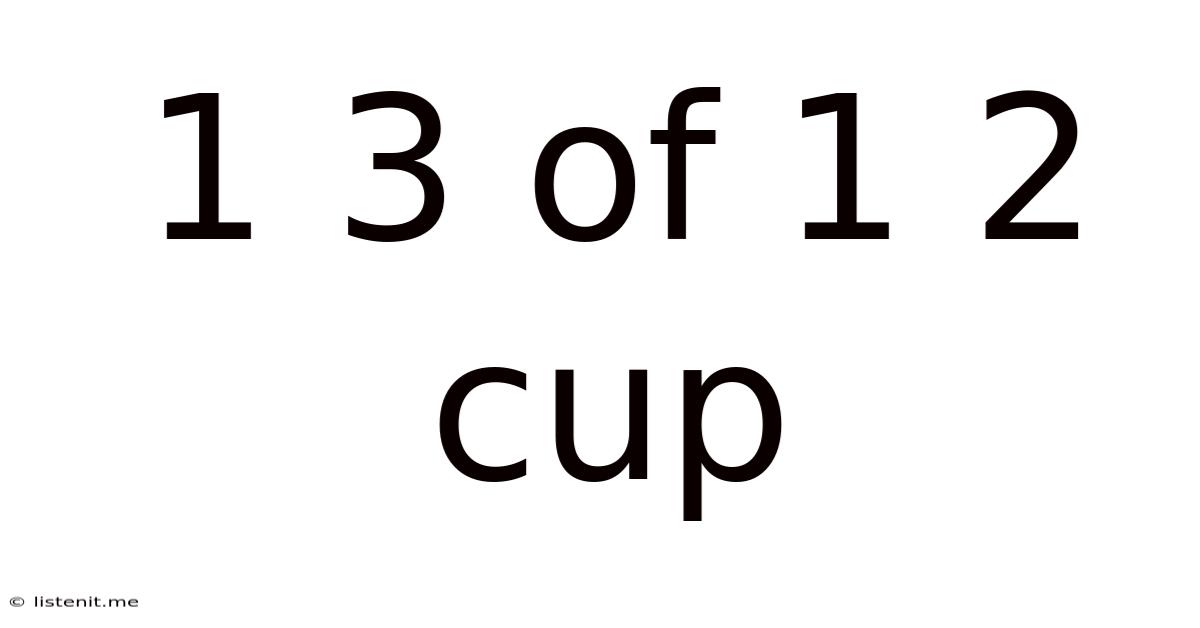
Table of Contents
Decoding the Mystery: Understanding "1 ⅓ of 1 ½ Cups"
The seemingly simple phrase "1 ⅓ of 1 ½ cups" can be surprisingly confusing, especially when dealing with recipes or measurements requiring precision. This article will break down this fractional calculation step-by-step, exploring various methods of solving it and providing valuable context for similar problems in everyday life. We'll also delve into the importance of accurate measurements in cooking and other fields, exploring the potential consequences of inaccuracies. Finally, we'll explore the broader mathematical concepts involved, making this a comprehensive guide to understanding and tackling such fractional problems.
Understanding the Problem: Fractions and Mixed Numbers
Before we dive into the calculation, let's refresh our understanding of fractions and mixed numbers. The problem presents two mixed numbers: 1 ⅓ and 1 ½.
- Mixed numbers combine a whole number and a fraction (e.g., 1 ½).
- Fractions represent parts of a whole (e.g., ⅓, ½).
To solve "1 ⅓ of 1 ½ cups," we need to interpret "of" as multiplication. Therefore, the problem translates to: 1 ⅓ x 1 ½.
Method 1: Converting to Improper Fractions
The most straightforward method involves converting the mixed numbers into improper fractions. Improper fractions have a numerator larger than or equal to the denominator.
Step 1: Convert 1 ⅓ to an improper fraction:
- Multiply the whole number (1) by the denominator (3): 1 x 3 = 3
- Add the numerator (1): 3 + 1 = 4
- Keep the same denominator (3): The improper fraction is ⁴⁄₃.
Step 2: Convert 1 ½ to an improper fraction:
- Multiply the whole number (1) by the denominator (2): 1 x 2 = 2
- Add the numerator (1): 2 + 1 = 3
- Keep the same denominator (2): The improper fraction is ³⁄₂.
Step 3: Multiply the improper fractions:
- Multiply the numerators: 4 x 3 = 12
- Multiply the denominators: 3 x 2 = 6
- The result is ¹²⁄₆.
Step 4: Simplify the fraction:
- Divide both the numerator and the denominator by their greatest common divisor (GCD), which is 6: 12 ÷ 6 = 2 and 6 ÷ 6 = 1
- The simplified fraction is ²⁄₁, which equals 2.
Therefore, 1 ⅓ of 1 ½ cups is equal to 2 cups.
Method 2: Using Decimal Equivalents
Another approach involves converting the mixed numbers to their decimal equivalents and then multiplying.
Step 1: Convert 1 ⅓ to a decimal:
- Divide the numerator (1) by the denominator (3): 1 ÷ 3 ≈ 0.333
- Add the whole number (1): 1 + 0.333 ≈ 1.333
Step 2: Convert 1 ½ to a decimal:
- Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
- Add the whole number (1): 1 + 0.5 = 1.5
Step 3: Multiply the decimals:
- Multiply the decimal equivalents: 1.333 x 1.5 ≈ 1.9995
Step 4: Round the result:
- Since we're dealing with measurements, rounding to the nearest whole number is appropriate.
- 1.9995 rounds to 2.
Therefore, 1 ⅓ of 1 ½ cups is approximately 2 cups. Note that slight discrepancies can occur due to rounding in decimal conversions.
The Importance of Accurate Measurement
The accuracy of measurements is paramount in various fields, especially cooking, baking, pharmaceuticals, and engineering. In cooking, for example, precise measurements can significantly impact the outcome of a recipe. Using too much or too little of an ingredient can alter the taste, texture, and overall success of a dish.
For instance, in baking, the ratio of ingredients is crucial. A slight deviation in the amount of leavening agent, for example, could result in a cake that is either too flat or too dense. Similarly, in pharmaceuticals, inaccurate measurements can have serious consequences, potentially leading to ineffective or even dangerous medications.
Practical Applications and Real-World Examples
Understanding how to work with fractions and mixed numbers is crucial in many real-world scenarios. Beyond cooking, consider these examples:
- Construction and DIY: Calculating material quantities for building projects requires precise measurements to avoid waste and ensure structural integrity.
- Sewing and Tailoring: Accurate fabric measurements are vital for creating well-fitting garments.
- Gardening: Determining the correct amount of fertilizer or pesticide for a garden relies on understanding and applying fractional measurements.
- Finance: Calculating percentages, interest rates, and proportions in personal finance or investments involves working with fractions and decimals.
Beyond the Calculation: Mastering Fraction Operations
The problem of "1 ⅓ of 1 ½ cups" highlights the importance of understanding fundamental fraction operations. Here's a quick refresher:
- Adding and Subtracting Fractions: Requires finding a common denominator.
- Multiplying Fractions: Multiply the numerators together and the denominators together.
- Dividing Fractions: Invert the second fraction and multiply.
Conclusion: Mastering Fractions for a More Precise World
This article has demonstrated several methods for solving the problem "1 ⅓ of 1 ½ cups," highlighting the practical applications and importance of accurate measurement in everyday life. Whether you're a baker, a builder, or simply someone who wants to be more comfortable working with fractions, mastering these skills provides a solid foundation for tackling more complex mathematical problems and making more precise calculations in your daily activities. The ability to confidently work with fractions and mixed numbers empowers you to approach various tasks with greater accuracy and precision, leading to better outcomes in numerous areas of life. Remember that practice makes perfect – the more you work with fractions, the more comfortable and confident you'll become.
Latest Posts
Latest Posts
-
What Factors Govern The Position Of An Ir Absorption Peak
May 10, 2025
-
Can An Element Be Broken Down Into A Simpler Substance
May 10, 2025
-
The Most Specific Level Of Classification
May 10, 2025
-
5 7 Divided By 3 4
May 10, 2025
-
What Is 5 7 In Decimal Form
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 1 2 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.