5 7 Divided By 3 4
listenit
May 10, 2025 · 5 min read
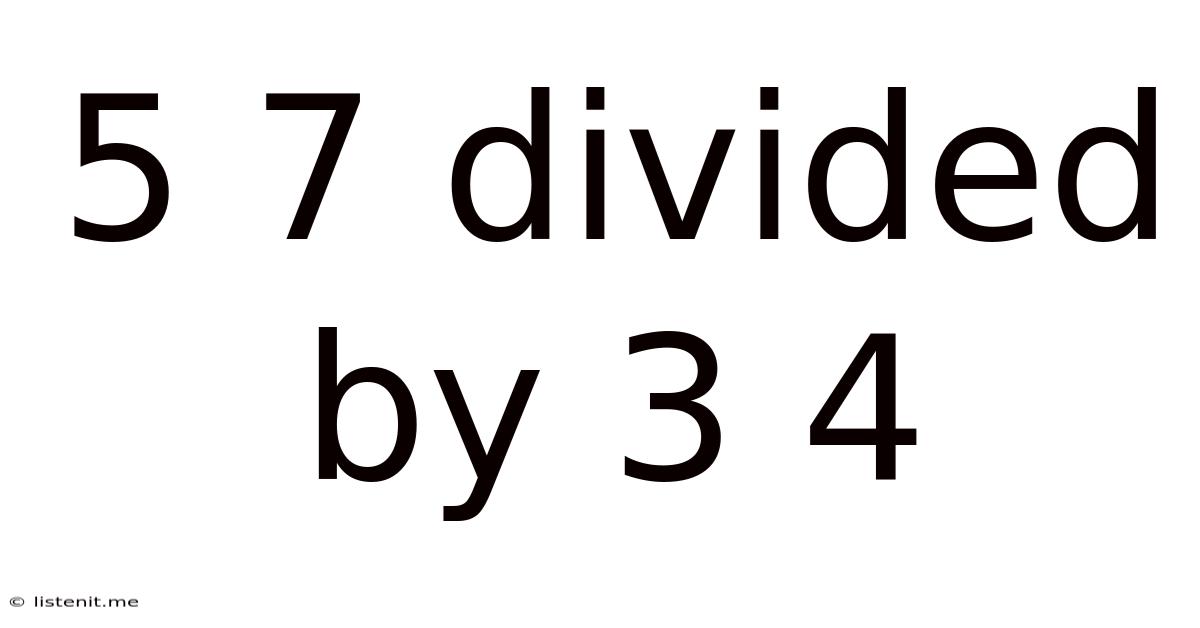
Table of Contents
Decoding the Mathematical Enigma: 5/7 Divided by 3/4
The seemingly simple mathematical expression "5/7 divided by 3/4" can, at first glance, appear intimidating. However, understanding the underlying principles of fraction division reveals a surprisingly straightforward solution. This article will not only delve into the mechanics of solving this particular problem but also explore the broader concepts of fraction manipulation and their real-world applications. We'll also touch upon strategies for optimizing your approach to such problems and provide practical examples to solidify your understanding.
Understanding Fractions: A Foundation for Division
Before tackling the division problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 5/7, 5 is the numerator and 7 is the denominator. This signifies that we have 5 parts out of a total of 7 equal parts.
The Mechanics of Fraction Division: Inverting and Multiplying
Dividing fractions isn't about directly dividing the numerators and denominators. Instead, we employ a clever technique: inverting the second fraction (the divisor) and then multiplying. This method is derived from the fundamental principles of reciprocals and their interaction with division.
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
Therefore, to solve 5/7 divided by 3/4, we follow these steps:
-
Invert the divisor: The divisor is 3/4. Its reciprocal is 4/3.
-
Change the division sign to a multiplication sign: Our expression now becomes: 5/7 * 4/3
-
Multiply the numerators together: 5 * 4 = 20
-
Multiply the denominators together: 7 * 3 = 21
-
Simplify the resulting fraction (if possible): In this case, 20/21 is already in its simplest form as 20 and 21 share no common factors other than 1.
Therefore, the solution to 5/7 divided by 3/4 is 20/21.
Visualizing Fraction Division: A Practical Approach
While the mathematical process is efficient, visualizing the problem can aid understanding. Imagine you have 5/7 of a pizza. Dividing this by 3/4 means you're asking: "How many portions of 3/4 of a pizza fit into 5/7 of a pizza?" The answer, as we've calculated, is 20/21 portions. This means slightly less than one full portion of 3/4 pizza fits within 5/7 of a pizza.
Expanding the Concept: Complex Fraction Division
The principles discussed above can be extended to more complex problems involving mixed numbers or decimals. Let's consider an example:
Problem: 2 1/3 divided by 1.5
Solution:
-
Convert mixed numbers to improper fractions: 2 1/3 becomes 7/3.
-
Convert decimals to fractions: 1.5 becomes 3/2.
-
Invert and multiply: 7/3 divided by 3/2 becomes 7/3 * 2/3
-
Multiply numerators and denominators: (7 * 2) / (3 * 3) = 14/9
-
Simplify or convert to a mixed number: 14/9 can be simplified to 1 5/9.
Thus, 2 1/3 divided by 1.5 equals 1 5/9.
Real-World Applications of Fraction Division
Fraction division isn't confined to the classroom; it finds practical application in various real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down often involves dividing fractions. If a recipe calls for 2/3 cup of flour and you want to halve the recipe, you'll need to divide 2/3 by 2.
-
Construction and Engineering: Precise measurements are crucial in construction. Dividing fractions helps in accurately calculating materials needed for projects.
-
Sewing and Fabric Design: Cutting fabric involves precise measurements, and fraction division ensures accurate calculations for pattern pieces.
-
Finance and Budgeting: Dividing your budget into fractional portions for different expenses requires understanding fraction division.
-
Data Analysis: Many data sets involve fractions, and analyzing them often involves division of fractions.
Strategies for Mastering Fraction Division
To excel in fraction division, consider these strategies:
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Start with simple problems and gradually increase the complexity.
-
Visual Aids: Using visual aids, like diagrams or physical objects, can help visualize the problem and enhance understanding.
-
Break Down Complex Problems: When faced with a complex problem, break it down into smaller, manageable steps.
-
Utilize Online Resources: Many online resources, such as educational websites and videos, can provide additional practice and explanations.
-
Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or classmates if you're struggling with a particular concept.
Beyond the Basics: Advanced Fraction Operations
While this article focused on division, understanding other fraction operations—addition, subtraction, and multiplication—is equally important. These operations form the foundation for more complex mathematical problems involving fractions. Mastering these basic operations will significantly improve your ability to tackle advanced mathematical concepts in various fields.
Conclusion: Embracing the Power of Fractions
Fraction division, though initially appearing daunting, is a fundamental mathematical skill with broad applications. By understanding the principles of inverting and multiplying, and by employing effective strategies, you can confidently tackle any fraction division problem. Remember that practice is key, and visualizing the problem can greatly enhance understanding. Mastering this skill will not only improve your mathematical abilities but also equip you with a valuable tool for tackling real-world challenges. The seemingly simple expression "5/7 divided by 3/4," therefore, unlocks a deeper understanding of fractions and their practical significance in our daily lives. From scaling recipes to calculating material needs in construction projects, the ability to confidently perform fraction division is an invaluable skill that extends far beyond the confines of the classroom.
Latest Posts
Latest Posts
-
How Many Inches Is 1 3 Of A Yard
May 10, 2025
-
Acetic Acid And Sodium Acetate Reaction
May 10, 2025
-
How To Find The Equation Of A Vertical Line
May 10, 2025
-
The Rna Base Complementary To A In Dna Is
May 10, 2025
-
How Did Moseley Arrange The Elements In The Periodic Table
May 10, 2025
Related Post
Thank you for visiting our website which covers about 5 7 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.