1/3 + 3/5 As A Fraction
listenit
May 23, 2025 · 5 min read
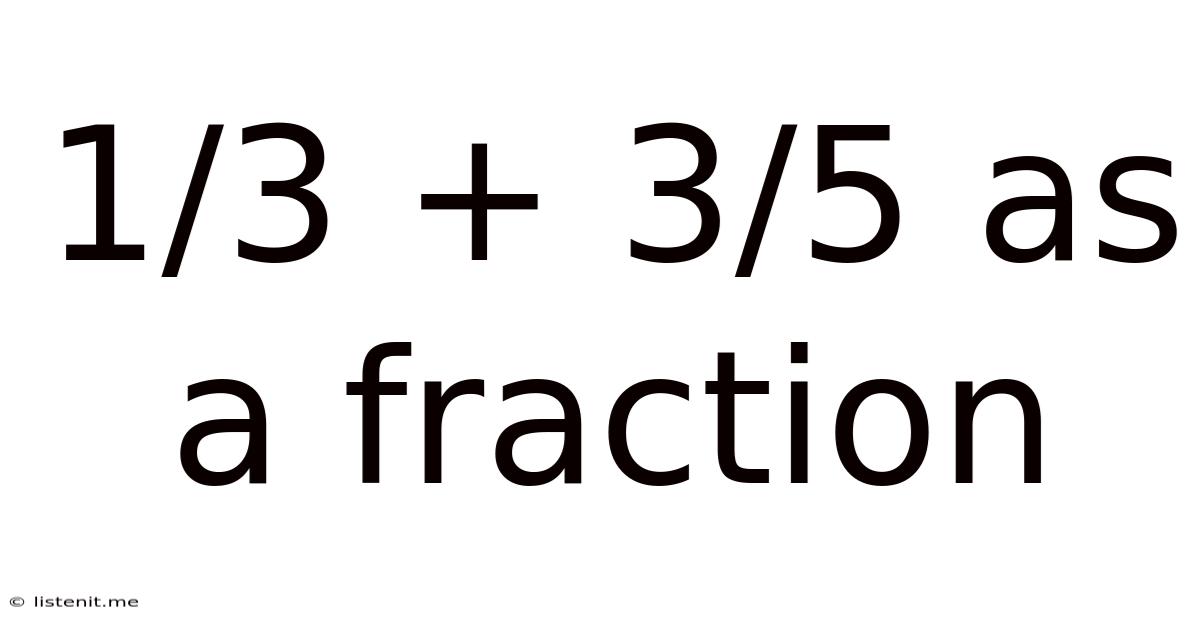
Table of Contents
1/3 + 3/5 as a Fraction: A Comprehensive Guide to Adding Fractions
Adding fractions might seem like a simple arithmetic task, but mastering the process is crucial for a strong foundation in mathematics. This comprehensive guide will delve deep into the addition of fractions, specifically tackling the problem of 1/3 + 3/5, while also exploring the broader concepts and techniques involved. We'll break down the steps, explain the underlying principles, and offer various approaches to solve similar problems. By the end, you'll not only understand how to solve 1/3 + 3/5, but you'll also possess the skills to confidently tackle any fraction addition problem.
Understanding Fractions
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) represents one part, and the denominator (3) indicates that the whole is divided into three equal parts.
Finding a Common Denominator
The core principle of adding fractions lies in finding a common denominator. This is a crucial step because you can only add or subtract fractions when they share the same denominator. A common denominator is a number that is a multiple of both denominators.
In our problem, 1/3 + 3/5, the denominators are 3 and 5. To find the least common denominator (LCD), we look for the smallest number that is divisible by both 3 and 5. One method is to list the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 5: 5, 10, 15, 20, 25...
The smallest number that appears in both lists is 15. Therefore, the least common denominator (LCD) for 1/3 and 3/5 is 15.
Converting Fractions to Equivalent Fractions
Once we have the common denominator (15), we need to convert both fractions, 1/3 and 3/5, into equivalent fractions with a denominator of 15. To do this, we multiply both the numerator and the denominator of each fraction by the same number:
-
For 1/3: To get a denominator of 15, we multiply both the numerator and denominator by 5 (because 3 x 5 = 15): (1 x 5) / (3 x 5) = 5/15
-
For 3/5: To get a denominator of 15, we multiply both the numerator and denominator by 3 (because 5 x 3 = 15): (3 x 3) / (5 x 3) = 9/15
Adding the Fractions
Now that both fractions have the same denominator (15), we can add them:
5/15 + 9/15 = (5 + 9) / 15 = 14/15
Therefore, 1/3 + 3/5 = 14/15
Simplifying Fractions (If Necessary)
In some cases, after adding fractions, the resulting fraction might be able to be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In our case, 14/15 is already in its simplest form because 14 and 15 share no common divisors other than 1.
Alternative Methods for Finding the Least Common Denominator
While listing multiples is a straightforward method, especially for smaller numbers, other techniques are useful for larger numbers or when dealing with multiple fractions:
Prime Factorization
This method involves breaking down each denominator into its prime factors. The LCD is then found by taking the highest power of each prime factor present in the denominators.
For example:
- 3 = 3
- 5 = 5
The prime factors are 3 and 5. The LCD is 3 x 5 = 15.
Using the Formula: LCD = (a x b) / GCD(a, b)
This formula uses the greatest common divisor (GCD) of the two denominators. The GCD is the largest number that divides both numbers without leaving a remainder. There are several ways to find the GCD, including the Euclidean algorithm.
For 3 and 5, the GCD is 1 (as they are coprime). Therefore, the LCD = (3 x 5) / 1 = 15.
Practical Applications of Fraction Addition
Understanding fraction addition extends beyond simple arithmetic problems. It has significant applications in various real-world scenarios:
-
Baking and Cooking: Recipes often involve fractional measurements of ingredients. Adding fractions is essential for accurate calculations.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Fractions are frequently used to represent dimensions and quantities.
-
Finance: Working with budgets and financial statements involves dealing with fractions and percentages.
-
Science: Many scientific calculations, particularly in fields like chemistry and physics, require manipulating fractions.
Advanced Fraction Operations: Multiplication and Division
While this guide focuses on addition, it's important to acknowledge the related operations of multiplication and division of fractions:
Multiplication of Fractions
To multiply fractions, simply multiply the numerators together and the denominators together. For example: (1/3) x (3/5) = (1 x 3) / (3 x 5) = 3/15 = 1/5
Division of Fractions
To divide fractions, invert the second fraction (the divisor) and then multiply. For example: (1/3) / (3/5) = (1/3) x (5/3) = 5/9
Conclusion: Mastering Fraction Addition
Adding fractions, particularly a problem like 1/3 + 3/5, requires a thorough understanding of fundamental concepts such as finding common denominators and converting fractions to equivalent forms. By mastering these techniques, you'll build a solid foundation in arithmetic and gain the ability to solve a wide range of fraction problems confidently. Remember to always simplify your answer to its lowest terms for the most accurate and concise representation. The practice of these methods will ultimately lead to proficiency in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Many Hours In 12 Years
May 23, 2025
-
December 17 Day Of The Week
May 23, 2025
-
What Is 1 2 Of 5 8
May 23, 2025
-
1959 To 2024 How Many Years Age
May 23, 2025
-
How Many Ww Points Per Day For A Man 2023
May 23, 2025
Related Post
Thank you for visiting our website which covers about 1/3 + 3/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.