What Is 1 2 Of 5 8
listenit
May 23, 2025 · 5 min read
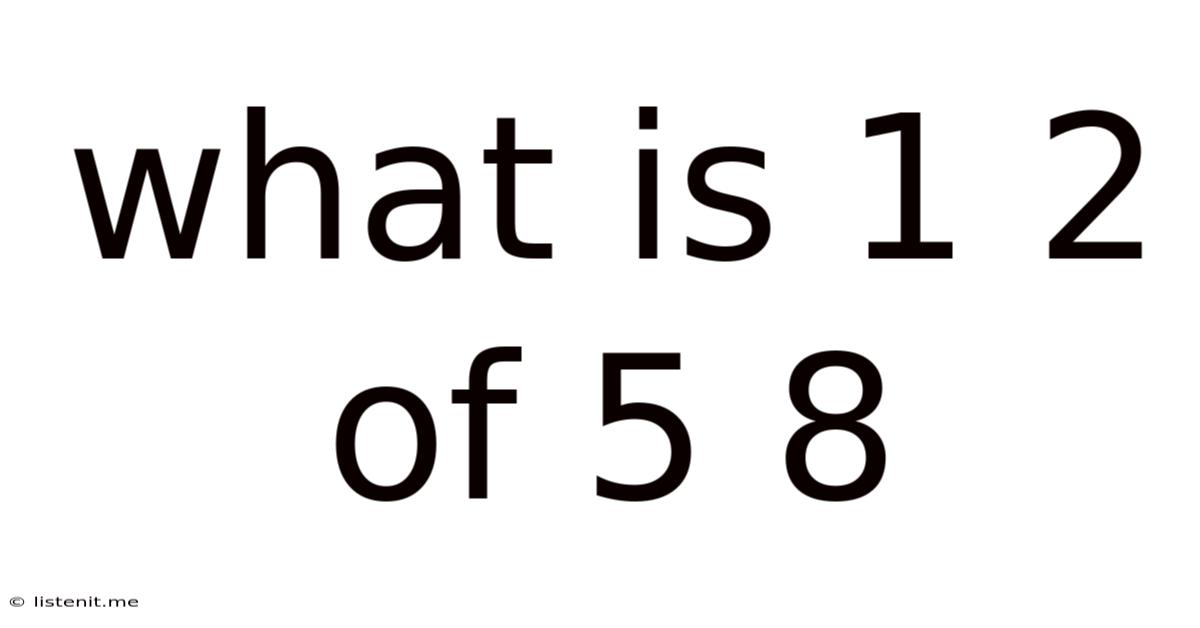
Table of Contents
What is 1/2 of 5/8? A Comprehensive Guide to Fraction Multiplication
Understanding fractions and how to perform operations like multiplication on them is a fundamental skill in mathematics. This comprehensive guide will delve into the question, "What is 1/2 of 5/8?", providing a step-by-step explanation, exploring related concepts, and offering practical applications to solidify your understanding.
Understanding the Problem: 1/2 of 5/8
The phrase "1/2 of 5/8" translates directly into a multiplication problem: (1/2) * (5/8). This means we need to find the product of the two fractions. Before jumping into the calculation, let's refresh our understanding of fractions.
A Quick Refresher on Fractions
A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator (we have 3 parts), and 4 is the denominator (the whole is divided into 4 equal parts).
Multiplying Fractions: A Step-by-Step Approach
Multiplying fractions is a relatively straightforward process. Here's the method:
- Multiply the numerators: Multiply the top numbers of both fractions together.
- Multiply the denominators: Multiply the bottom numbers of both fractions together.
- Simplify the result (if possible): Reduce the resulting fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's apply this to our problem: (1/2) * (5/8)
- Multiply the numerators: 1 * 5 = 5
- Multiply the denominators: 2 * 8 = 16
- The result: 5/16
Therefore, 1/2 of 5/8 is 5/16.
Visualizing the Multiplication
Visualizing fractions can significantly aid in understanding the concept of multiplication. Imagine a rectangle representing the whole.
- 5/8: Divide the rectangle into 8 equal parts and shade 5 of them. This represents 5/8.
- 1/2 of 5/8: Now, take half (1/2) of the shaded area (5/8). This means dividing the shaded area into two equal parts and considering only one of those parts. You will find that this represents 5/16 of the original rectangle.
This visual representation helps solidify the concept that multiplying by a fraction less than 1 results in a smaller value.
Further Exploration of Fraction Multiplication
Let's examine some related concepts and variations to deepen your understanding.
Multiplying More Than Two Fractions
The method for multiplying two fractions extends seamlessly to multiplying three or more fractions. Simply multiply all the numerators together and all the denominators together. Then, simplify the resulting fraction if possible.
For example: (1/2) * (5/8) * (2/3) = (1 * 5 * 2) / (2 * 8 * 3) = 10/48. This fraction can be simplified to 5/24 by dividing both the numerator and denominator by 2 (their GCD).
Multiplying Fractions with Whole Numbers
A whole number can be represented as a fraction with a denominator of 1. For instance, 3 can be written as 3/1. To multiply a fraction by a whole number, simply multiply the numerator of the fraction by the whole number and keep the denominator the same.
Example: (1/2) * 3 = (1/2) * (3/1) = 3/2 = 1 1/2
Multiplying Mixed Numbers
Mixed numbers consist of a whole number and a fraction (e.g., 1 1/2). Before multiplying mixed numbers, it's essential to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Keep the same denominator.
Example: Convert 1 1/2 to an improper fraction: (1 * 2) + 1 = 3; the improper fraction is 3/2.
Real-World Applications of Fraction Multiplication
Understanding fraction multiplication is crucial for various real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you would multiply 1/2 by 2 (resulting in 1 cup of flour).
-
Construction and Engineering: Accurate measurements and calculations often involve fractions. Determining the length of materials or calculating the area of surfaces frequently necessitates fraction multiplication.
-
Finance: Calculating percentages, interest rates, and discounts frequently involves fraction manipulation.
-
Data Analysis: In data analysis, working with proportions and ratios often involves multiplication of fractions.
Troubleshooting Common Errors in Fraction Multiplication
-
Forgetting to Simplify: Always simplify the resulting fraction to its lowest terms by finding the GCD of the numerator and denominator.
-
Incorrectly Multiplying Numerators and Denominators: Double-check your multiplication to avoid errors.
-
Not Converting Mixed Numbers to Improper Fractions: Remember to convert mixed numbers to improper fractions before multiplication.
-
Misunderstanding the Concept of "Of": Remember that "of" in the context of fractions signifies multiplication.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a foundational skill with wide-ranging practical applications. By understanding the underlying principles, employing the step-by-step approach, and practicing regularly, you can confidently tackle fraction multiplication problems and apply this valuable skill in various contexts. Remember to visualize, practice, and always check your answers for simplification. The more you practice, the more comfortable and efficient you'll become. From cooking to construction, finance to data analysis, your proficiency in fraction multiplication will enhance your problem-solving capabilities across numerous domains. So, continue practicing and sharpening your skills – the rewards are well worth the effort.
Latest Posts
Latest Posts
-
Write The Number 280 In Scientific Notation
May 24, 2025
-
How Much Is A Mortgage On A 150k House
May 24, 2025
-
Greatest Common Factor Of 28 And 44
May 24, 2025
-
What Is 3 4 X 1 2
May 24, 2025
-
Voltage Drop Formula For 3 Phase
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.