1/2 Divided By 1/6 In Fraction Form
listenit
May 23, 2025 · 5 min read
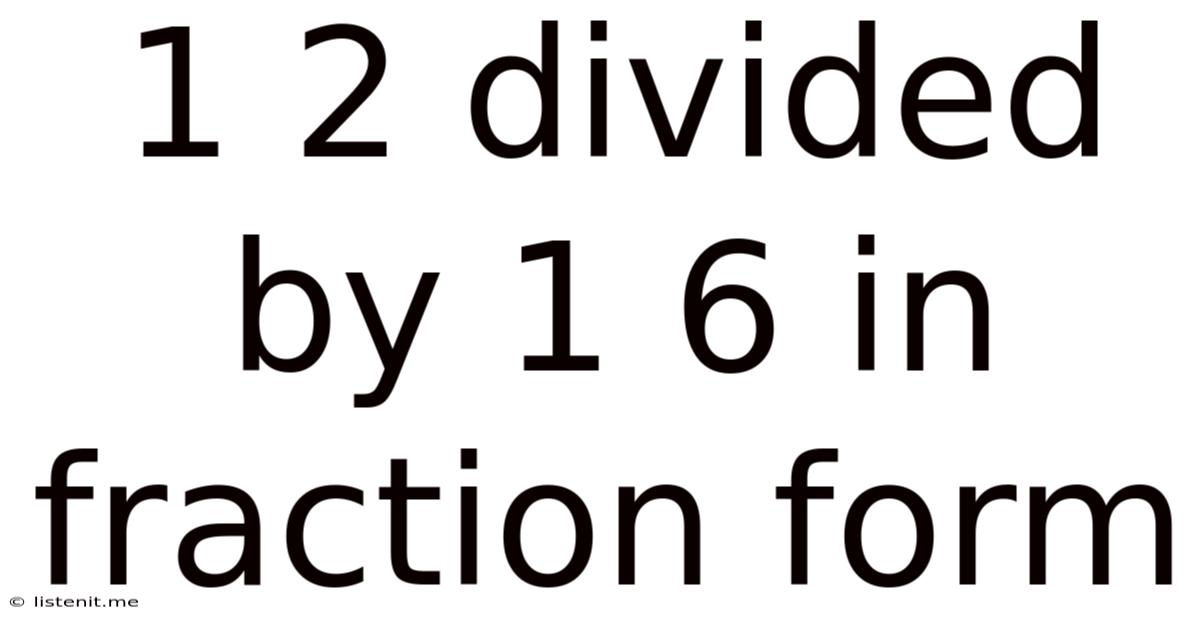
Table of Contents
1/2 Divided by 1/6 in Fraction Form: A Comprehensive Guide
Understanding fraction division can be tricky, but mastering it opens doors to more advanced mathematical concepts. This comprehensive guide will walk you through the process of dividing 1/2 by 1/6, explaining the underlying principles and offering various methods for solving similar problems. We'll cover not just the "how" but also the "why," ensuring a solid understanding that extends beyond this specific problem.
Understanding Fraction Division
Before diving into the specific problem of 1/2 ÷ 1/6, let's establish a strong foundation in fraction division. The key concept to remember is that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/6 is 6/1 (or simply 6).
This principle holds true because division is essentially the inverse operation of multiplication. When we divide by a fraction, we're asking, "How many times does this fraction fit into the other?" Multiplying by the reciprocal effectively answers this question.
Method 1: Using the Reciprocal
This is the most straightforward and commonly taught method. To solve 1/2 ÷ 1/6, we follow these steps:
-
Find the reciprocal of the second fraction: The reciprocal of 1/6 is 6/1 or 6.
-
Change the division to multiplication: Replace the division sign (÷) with a multiplication sign (×).
-
Multiply the fractions: Now we have (1/2) × (6/1). Multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 6) / (2 × 1) = 6/2
-
Simplify the result: 6/2 simplifies to 3.
Therefore, 1/2 ÷ 1/6 = 3.
Method 2: Using Common Denominators
While the reciprocal method is generally preferred for its efficiency, understanding the common denominator approach provides a deeper insight into fraction division. This method emphasizes the underlying concept of how many times one fraction fits into another.
-
Find a common denominator: For the fractions 1/2 and 1/6, the least common denominator (LCD) is 6.
-
Convert the fractions to equivalent fractions with the common denominator:
1/2 becomes 3/6 (multiply both numerator and denominator by 3) 1/6 remains 1/6
-
Divide the numerators: Now we divide the numerators: 3 ÷ 1 = 3.
This method shows that 3/6 (which is equivalent to 1/2) contains 1/6 three times. Therefore, 1/2 ÷ 1/6 = 3.
Method 3: Visual Representation
Visual aids can greatly enhance understanding, especially for those new to fractions. Imagine you have a half of a pizza (1/2). Now, imagine slices of pizza that are one-sixth (1/6) the size of the whole pizza. How many of these 1/6 slices fit into the 1/2 slice?
By drawing a visual representation, you'll easily see that three 1/6 slices fit perfectly into the 1/2 slice. This reinforces the answer: 1/2 ÷ 1/6 = 3.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving abstract math problems; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require dividing fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make only 1/6 of the recipe, you need to calculate (1/2) ÷ (1/6) to determine the amount of flour required.
-
Sewing and Crafting: Many craft projects involve precise measurements, often requiring the division of fractions to accurately cut materials.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering, with fractions frequently appearing in blueprints and calculations.
-
Data Analysis: Dividing fractions is essential in various data analysis techniques, where you might need to compare proportions or ratios.
Troubleshooting Common Mistakes
Several common mistakes can arise when dividing fractions. Let's address some of them:
-
Forgetting to use the reciprocal: One of the most prevalent errors is simply dividing the fractions directly without using the reciprocal of the second fraction. Remember, division is turned into multiplication by the reciprocal.
-
Incorrectly simplifying fractions: Make sure to simplify fractions to their lowest terms. Leaving the answer as 6/2 is not considered fully simplified.
-
Mistakes with multiplication: Errors can occur during the multiplication step. Double-check your work to ensure that the numerators and denominators are multiplied correctly.
Extending Your Understanding: Dividing More Complex Fractions
The principles discussed here can be extended to more complex fraction division problems. For instance, let's consider:
(3/4) ÷ (2/5)
-
Find the reciprocal of the second fraction: The reciprocal of 2/5 is 5/2.
-
Change the division to multiplication: (3/4) × (5/2)
-
Multiply the fractions: (3 × 5) / (4 × 2) = 15/8
-
Simplify (if necessary): The fraction 15/8 is already in its simplest form, but it could also be written as a mixed number: 1 7/8
Mastering Fraction Division: Practice Makes Perfect
Consistent practice is key to mastering fraction division. Start with simpler problems and gradually work your way towards more complex ones. Use various methods to solve the same problem to reinforce your understanding and identify the most efficient approach for you.
Conclusion
Dividing fractions, even seemingly simple ones like 1/2 ÷ 1/6, requires a solid grasp of fundamental principles. By understanding the reciprocal method, the common denominator approach, and the visual representation, you can effectively solve these problems and apply them in various real-world situations. Remember to practice regularly and address common errors to build confidence and fluency in fraction division. With consistent effort, you’ll not only solve this specific problem but will also gain a comprehensive understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
5 7 Divided By 1 3
May 23, 2025
-
What Is 7 Divided By 100
May 23, 2025
-
What Is 14 Days From Todays Date
May 23, 2025
-
How Many Points Is 10 Percent Of Your Grade
May 23, 2025
-
The Value Of One Currency Expressed In Terms Of Another
May 23, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 1/6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.