5 7 Divided By 1 3
listenit
May 23, 2025 · 4 min read
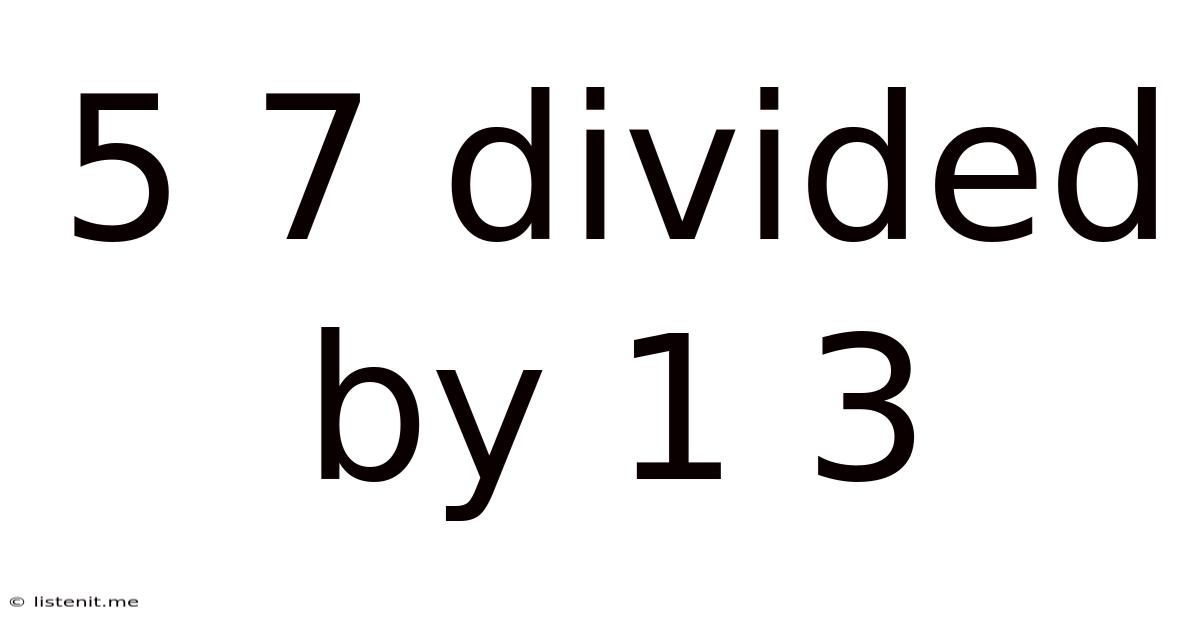
Table of Contents
5/7 Divided by 1/3: A Deep Dive into Fraction Division
This article will thoroughly explore the seemingly simple mathematical problem of 5/7 divided by 1/3. While the calculation itself is straightforward, we'll delve into the underlying principles, explore various methods for solving it, and examine its applications in real-world scenarios. Understanding this seemingly basic operation provides a solid foundation for more complex mathematical concepts.
Understanding Fraction Division
Before tackling 5/7 divided by 1/3 directly, let's solidify our understanding of fraction division. Unlike addition and subtraction, where we need common denominators, division of fractions involves a clever technique – inverting the second fraction and multiplying.
This method stems from the definition of division. Dividing by a fraction is the same as multiplying by its reciprocal (its multiplicative inverse). The reciprocal of a fraction is simply obtained by swapping its numerator and denominator. For example, the reciprocal of 1/3 is 3/1 (or simply 3).
Why Does This Work?
The reason behind inverting and multiplying is rooted in the fundamental properties of mathematics. Consider this example: 6 ÷ 2 = 3. This means that 2 fits into 6 three times. Now consider 6 ÷ (1/2) = ?. This is asking, "How many times does 1/2 fit into 6?" Clearly, 1/2 fits into 6 twelve times (6 x 2 = 12). Notice how we multiplied by the reciprocal of 1/2 (which is 2) to find the answer. This illustrates the core principle behind dividing fractions.
Solving 5/7 Divided by 1/3
Now, let's apply this understanding to solve 5/7 divided by 1/3:
-
Identify the divisor: The divisor is the fraction we are dividing by – in this case, 1/3.
-
Find the reciprocal: The reciprocal of 1/3 is 3/1 (or simply 3).
-
Multiply: Instead of dividing, we multiply 5/7 by the reciprocal of 1/3:
(5/7) ÷ (1/3) = (5/7) x (3/1)
-
Multiply the numerators and the denominators:
(5 x 3) / (7 x 1) = 15/7
-
Simplify (if necessary): In this case, 15/7 is an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number:
15/7 = 2 1/7
Therefore, 5/7 divided by 1/3 equals 2 1/7.
Alternative Methods: Using Decimal Conversions
While inverting and multiplying is the most efficient method, we can also solve this problem using decimal conversions. First, convert both fractions to decimals:
- 5/7 ≈ 0.714
- 1/3 ≈ 0.333
Then perform the division:
0.714 ÷ 0.333 ≈ 2.144
This decimal approximation is close to our exact answer of 2 1/7 (approximately 2.143). However, the decimal method can lead to rounding errors, making the fraction method more accurate for exact results.
Real-World Applications: Dividing Resources
Understanding fraction division is crucial in many real-world scenarios. Consider the following examples:
-
Baking: A recipe calls for 5/7 of a cup of flour, and you only want to make 1/3 of the recipe. How much flour do you need? You would divide 5/7 by 1/3, resulting in 2 1/7 cups of flour.
-
Sewing: You have 5/7 of a meter of fabric, and each piece needs to be 1/3 of a meter long. How many pieces can you cut? Again, dividing 5/7 by 1/3 gives you 2 1/7 pieces. Since you can't cut a fraction of a piece, you can cut two complete pieces.
-
Resource Allocation: Imagine you have 5/7 of a budget allocated for a project, and you need to divide it among 3 teams equally. The share for each team can be calculated by dividing 5/7 by 1/3.
Expanding the Concept: More Complex Fraction Division Problems
The principles illustrated above can be extended to solve more complex problems involving multiple fractions. For instance, consider:
(2/5) ÷ (3/4) ÷ (1/2)
We solve these step-by-step, following the order of operations and inverting each divisor before multiplying:
-
(2/5) ÷ (3/4) = (2/5) x (4/3) = 8/15
-
(8/15) ÷ (1/2) = (8/15) x (2/1) = 16/15 = 1 1/15
The key is to always remember to invert the divisor and then multiply.
Conclusion: Mastering Fraction Division
Mastering fraction division, as illustrated by the simple yet insightful problem of 5/7 divided by 1/3, is foundational to numerous mathematical applications. By understanding the principles behind inverting and multiplying, and by practicing various methods, you can confidently tackle more complex fraction calculations and apply these skills to real-world scenarios. Remember, the ability to work fluently with fractions is a key component of mathematical literacy and problem-solving. Consistent practice and a solid understanding of the underlying concepts are the keys to success. Don't hesitate to revisit these steps and apply them to further strengthen your understanding of this crucial mathematical operation.
Latest Posts
Latest Posts
-
0 5 Rounded To The Nearest Hundredth
May 23, 2025
-
Lowest Common Multiple Of 2 And 3
May 23, 2025
-
What Is 7 Of An Hour
May 23, 2025
-
5 1 3 2 2 3
May 23, 2025
-
What Is The Value Of 1310 In Binary
May 23, 2025
Related Post
Thank you for visiting our website which covers about 5 7 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.