1/2 + 3/8 How To Solve
listenit
Mar 26, 2025 · 5 min read
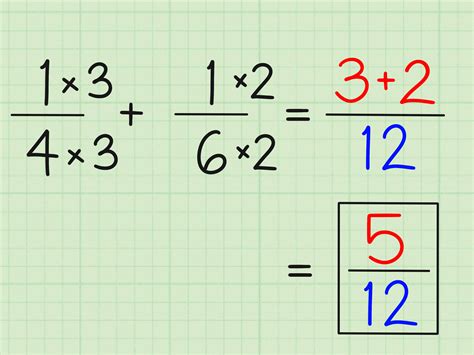
Table of Contents
1/2 + 3/8: A Comprehensive Guide to Solving Fraction Addition
Adding fractions might seem daunting at first, but with a structured approach and a clear understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through solving the equation 1/2 + 3/8, explaining the steps involved and providing valuable insights into fraction addition in general. We'll cover various methods, ensuring you grasp the fundamental concepts and can confidently tackle similar problems in the future.
Understanding the Basics of Fraction Addition
Before diving into the specific problem of 1/2 + 3/8, let's review the core concepts of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
Adding fractions requires a crucial step: finding a common denominator. This means expressing both fractions with the same denominator before adding the numerators. This step ensures we are adding parts of the same size, leading to an accurate sum.
Method 1: Finding the Least Common Denominator (LCD)
This is the most common and generally preferred method for adding fractions. The least common denominator is the smallest number that is a multiple of both denominators.
Steps:
-
Identify the denominators: In our problem, 1/2 + 3/8, the denominators are 2 and 8.
-
Find the least common multiple (LCM): The multiples of 2 are 2, 4, 6, 8, 10... The multiples of 8 are 8, 16, 24... The smallest number that appears in both lists is 8. Therefore, the least common denominator (LCD) is 8.
-
Convert the fractions to equivalent fractions with the LCD:
-
For 1/2, we need to multiply both the numerator and denominator by 4 to get a denominator of 8: (1 x 4) / (2 x 4) = 4/8
-
3/8 already has a denominator of 8, so it remains unchanged.
-
-
Add the numerators: Now that both fractions have the same denominator, we can simply add their numerators: 4/8 + 3/8 = (4 + 3)/8 = 7/8
Therefore, 1/2 + 3/8 = 7/8
Method 2: Using Prime Factorization to Find the LCD
This method is particularly helpful when dealing with larger denominators or when finding the LCD isn't immediately obvious.
Steps:
-
Find the prime factorization of each denominator:
- 2 = 2
- 8 = 2 x 2 x 2 = 2³
-
Identify the highest power of each prime factor: The only prime factor is 2, and its highest power is 2³ = 8.
-
The LCD is the product of the highest powers of all prime factors: In this case, the LCD is 8.
-
Follow steps 3 and 4 from Method 1 to convert the fractions and add the numerators.
Method 3: Visual Representation using Diagrams
Visual aids can be incredibly helpful, particularly for beginners. Let's represent the fractions using a diagram:
Imagine a circle divided into 8 equal parts.
-
1/2: This represents 4 out of 8 parts (half of the circle).
-
3/8: This represents 3 out of 8 parts.
Adding the shaded areas together (4 parts + 3 parts) gives us a total of 7 parts out of 8. Therefore, 1/2 + 3/8 = 7/8.
Simplifying Fractions (If Necessary)
Once you've added the fractions, always check if the resulting fraction can be simplified. A fraction is simplified when the numerator and denominator have no common factors other than 1. In our case, 7/8 is already in its simplest form because 7 and 8 have no common factors greater than 1.
Applying the Concept to More Complex Problems
The principles discussed here extend to more complex fraction addition problems. The key is always to find a common denominator before adding the numerators. Let's consider a more challenging example:
1/3 + 2/5 + 1/6
-
Find the LCD: The prime factorization method is particularly useful here.
- 3 = 3
- 5 = 5
- 6 = 2 x 3 The LCD is 2 x 3 x 5 = 30
-
Convert fractions to equivalent fractions with the LCD:
- 1/3 = (1 x 10) / (3 x 10) = 10/30
- 2/5 = (2 x 6) / (5 x 6) = 12/30
- 1/6 = (1 x 5) / (6 x 5) = 5/30
-
Add the numerators: 10/30 + 12/30 + 5/30 = (10 + 12 + 5)/30 = 27/30
-
Simplify: 27/30 can be simplified by dividing both numerator and denominator by 3: 27/30 = 9/10
Therefore, 1/3 + 2/5 + 1/6 = 9/10
Troubleshooting Common Mistakes
-
Forgetting to find a common denominator: This is the most frequent error. Remember, you cannot directly add numerators unless the denominators are the same.
-
Incorrectly finding the LCD: Double-check your calculations to ensure you've found the least common multiple.
-
Errors in converting fractions: Be meticulous when multiplying the numerator and denominator to obtain equivalent fractions.
-
Failing to simplify: Always simplify the resulting fraction to its lowest terms.
Conclusion: Mastering Fraction Addition
Adding fractions is a fundamental skill in mathematics with numerous practical applications. By understanding the concepts of numerators, denominators, and least common denominators, and by employing the methods outlined in this guide, you can confidently tackle fraction addition problems of varying complexities. Practice is key; the more you work with fractions, the more comfortable and proficient you'll become. Remember to always check your work for accuracy and simplification. With consistent effort and a methodical approach, mastering fraction addition will be within your reach. The solution to 1/2 + 3/8, as demonstrated, is 7/8, a result you can now confidently achieve and explain.
Latest Posts
Latest Posts
-
2002 Ap Chem Frq Form B
Mar 29, 2025
-
Where Is The Majority Of Earths Freshwater Located
Mar 29, 2025
-
What Kinds Of Elements Form Covalent Bonds
Mar 29, 2025
-
Why Water Is Liquid At Room Temperature
Mar 29, 2025
-
Examples Of Combustion In Everyday Life
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 3/8 How To Solve . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
