Z 1 X 2 Y 2
listenit
Jun 15, 2025 · 5 min read
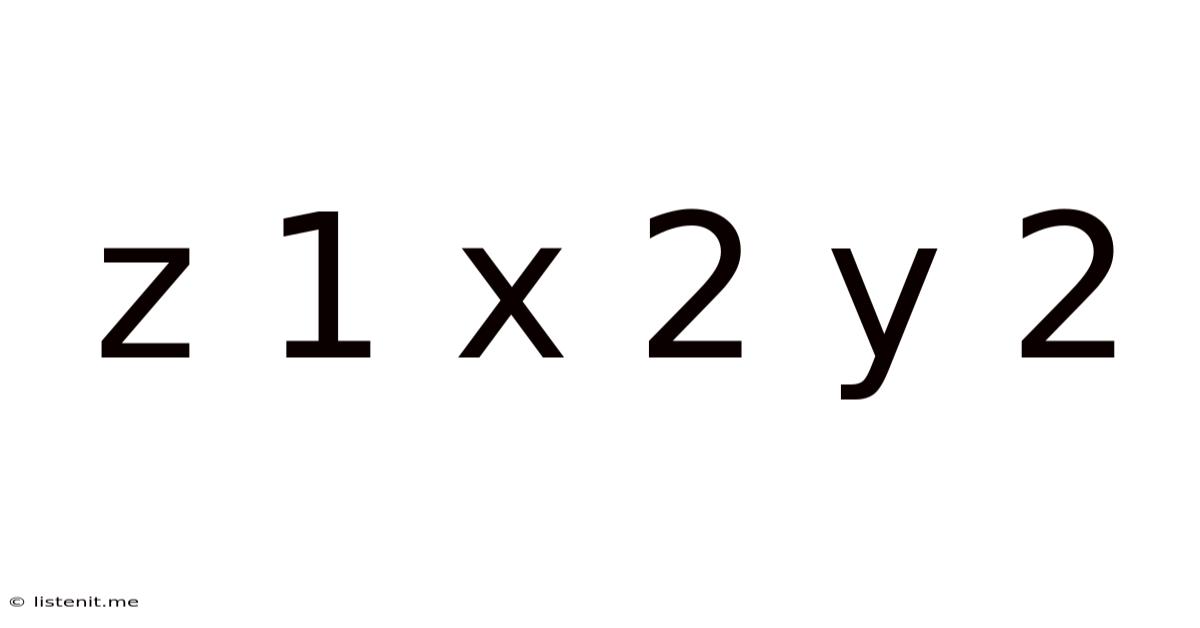
Table of Contents
Decoding the Enigma: A Deep Dive into Z=1x²y²
The seemingly simple algebraic expression, Z = 1x²y², presents a rich landscape for exploration across multiple mathematical disciplines. While its basic form might appear straightforward, delving into its properties reveals fascinating connections to geometry, calculus, and even advanced concepts like multivariable functions and their visualizations. This comprehensive article will dissect this expression, exploring its characteristics, applications, and implications.
Understanding the Fundamentals: Z = x²y²
At its core, Z = 1x²y² (which simplifies to Z = x²y²) represents a multivariable function. This means the value of Z is dependent on the values of two independent variables, x and y. Unlike single-variable functions where we might graph a curve, this expression describes a surface in three-dimensional space. The shape and properties of this surface are the central focus of our investigation.
Key Characteristics:
- Quadratic Nature: The presence of x² and y² signifies a quadratic relationship. This implies that changes in x and y will have a squared effect on Z. Small changes in x or y will result in proportionally larger changes in Z.
- Non-linearity: The function is inherently non-linear. This means that its graph isn't a straight line or a plane. Instead, it forms a curved surface.
- Symmetry: The function exhibits symmetry with respect to both the x and y axes. This means that Z(x, y) = Z(-x, y) = Z(x, -y) = Z(-x, -y). The surface is mirrored across both axes.
- Positive Values: Since both x² and y² are always non-negative, Z will always be non-negative (Z ≥ 0). The surface lies entirely above or on the xy-plane.
- Origin as a Critical Point: The point (0, 0, 0) is a critical point of the function, where both partial derivatives are zero. This point represents the minimum value of the function.
Visualizing the Surface: A 3D Representation
Understanding the behavior of Z = x²y² requires visualizing its three-dimensional graph. While precise graphical representations are best created using specialized software, we can conceptualize its key features:
- Parabolic Trough: Along the x-axis (when y = 0) and the y-axis (when x = 0), the function reduces to Z = 0, forming parabolic troughs.
- Curved Surface: As we move away from the axes, the value of Z increases, resulting in a curved surface that rises upwards.
- Increasing Steepness: The steepness of the surface increases as we move further from the origin. The rate of change in Z becomes more pronounced.
- No Asymptotes: The function does not have any asymptotes, meaning the surface doesn't approach any specific lines or planes as x or y approach infinity.
Mathematical Explorations: Calculus and Beyond
The power of calculus allows us to analyze the behavior of Z = x²y² in greater depth.
Partial Derivatives:
Calculating the partial derivatives provides crucial information about the slope of the surface in different directions:
- ∂Z/∂x = 2xy²: This represents the instantaneous rate of change of Z with respect to x, holding y constant.
- ∂Z/∂y = 2x²y: This represents the instantaneous rate of change of Z with respect to y, holding x constant.
Analyzing these partial derivatives helps identify critical points, regions of increase and decrease, and the overall behavior of the surface.
Gradient Vector:
The gradient vector, ∇Z = (2xy², 2x²y), provides a vector pointing in the direction of the steepest ascent of the surface at any given point (x, y). This vector is crucial in optimization problems where we seek to find the maximum or minimum values of the function.
Hessian Matrix:
The Hessian matrix, a matrix of second-order partial derivatives, is used to classify critical points as minima, maxima, or saddle points. For Z = x²y², the Hessian matrix can be used to confirm that (0,0) is a minimum point.
Applications in Optimization:
The function Z = x²y² can be incorporated into various optimization problems. For example, it might represent a utility function in economics or a cost function in engineering. Finding the maximum or minimum of this function subject to constraints is a common task in optimization theory.
Extending the Exploration: Variations and Generalizations
The simple expression Z = x²y² can serve as a foundation for exploring more complex scenarios.
Variations in Coefficients:
Introducing coefficients before x² and y² would change the shape and scale of the surface. For example, Z = ax²y², where 'a' is a constant, will alter the rate at which the surface rises or falls.
Higher-Order Terms:
Adding higher-order terms like x⁴y², x²y⁴, or higher powers would result in a significantly more complex surface with potentially multiple minima, maxima, and saddle points.
Incorporating Other Functions:
Combining x²y² with other functions can create even more intricate surfaces with diverse characteristics.
Real-World Applications:
While Z = x²y² might seem abstract, it has implications in various real-world applications.
- Physics: This type of function can model various physical phenomena, such as the distribution of energy or the intensity of a field.
- Engineering: Optimization problems in engineering often involve functions similar to Z = x²y², where minimizing or maximizing a certain quantity is the goal.
- Economics: In economics, utility functions, representing the satisfaction a consumer derives from goods and services, can take similar forms.
- Computer Graphics: This type of function is fundamental in creating 3D models and surfaces in computer graphics and animation.
Conclusion: Unveiling the Richness of Z = x²y²
The seemingly simple algebraic expression Z = x²y² offers a compelling journey into the world of multivariable functions. Through exploration of its properties, visualization of its surface, and application of calculus, we unveil a landscape of mathematical richness. Its fundamental nature provides a solid groundwork for understanding more complex mathematical models and their diverse applications in various fields. From its symmetric nature to its applications in optimization, this function demonstrates the power and elegance found in even the simplest mathematical expressions. Further investigation into its variations and generalizations opens up a vast realm of mathematical possibilities and provides a valuable stepping stone for understanding more complex multivariable functions.
Latest Posts
Latest Posts
-
How Long Deck Stain To Dry
Jun 15, 2025
-
Can You Trade Pokemon On An Emulator
Jun 15, 2025
-
Can You Change Only One Tire
Jun 15, 2025
-
Can You Drill In Wood Filler
Jun 15, 2025
-
New Gfci Test Button Wont Push In
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Z 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.