Y 2x 5 Solve For X
listenit
May 11, 2025 · 5 min read
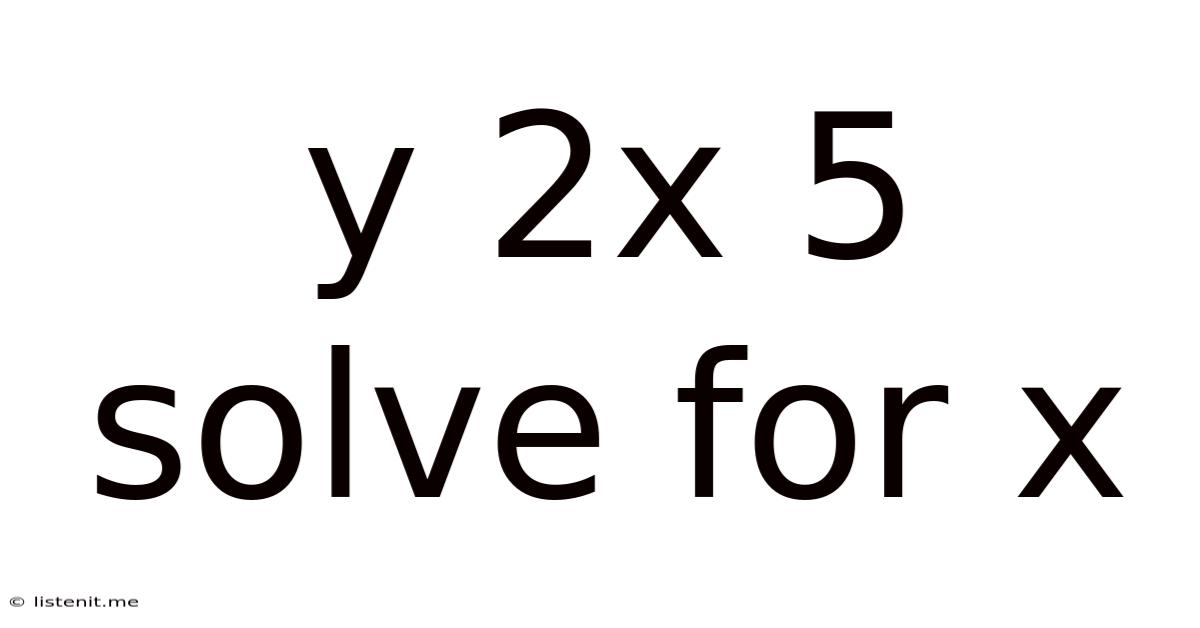
Table of Contents
Solving for x: A Comprehensive Guide to the Equation y = 2x + 5
The seemingly simple equation, y = 2x + 5, serves as a foundational concept in algebra. While its solution might seem straightforward, understanding the underlying principles and various approaches to solving for 'x' is crucial for mastering more complex algebraic problems. This comprehensive guide will delve into multiple methods, explain the reasoning behind each step, and provide examples to solidify your understanding. We'll also explore the broader implications of this equation in various mathematical contexts.
Understanding the Equation: y = 2x + 5
This equation represents a linear relationship between two variables, x and y. It's in the slope-intercept form (y = mx + b), where:
- y: Represents the dependent variable – its value depends on the value of x.
- x: Represents the independent variable – you can choose its value, and y will change accordingly.
- m (2 in this case): Represents the slope of the line. It indicates the rate at which y changes with respect to x. A slope of 2 means that for every one-unit increase in x, y increases by two units.
- b (5 in this case): Represents the y-intercept. It's the point where the line intersects the y-axis (where x = 0).
Understanding these components is key to visualizing the equation graphically and comprehending its behavior.
Method 1: Isolating x through Algebraic Manipulation
This is the most common and straightforward method. The goal is to isolate 'x' on one side of the equation by performing inverse operations.
Steps:
-
Subtract 5 from both sides: This removes the constant term from the right side, leaving only the term involving x. The equation becomes: y - 5 = 2x
-
Divide both sides by 2: This isolates x by removing the coefficient. The equation becomes: (y - 5) / 2 = x
-
Rearrange the equation: For clarity, we can rewrite the equation as: x = (y - 5) / 2
Therefore, the solution for x is x = (y - 5) / 2
This means that for any given value of y, you can calculate the corresponding value of x using this formula.
Example:
If y = 9, then x = (9 - 5) / 2 = 2.
Method 2: Using a Graphing Approach
While not directly "solving" for x algebraically, graphing provides a visual representation of the equation and allows you to find the x-value for a given y-value or vice-versa.
Steps:
-
Create a table of values: Choose several values for x, and calculate the corresponding y-values using the equation y = 2x + 5.
-
Plot the points: Plot the (x, y) coordinates on a graph.
-
Draw the line: Connect the points to form a straight line. This line visually represents all possible solutions to the equation.
-
Find x for a given y: If you have a specific value for y, locate that point on the y-axis, draw a horizontal line across to intersect the plotted line, then draw a vertical line down to the x-axis to find the corresponding x-value.
This method offers a visual understanding of the relationship between x and y but is less precise than algebraic methods for specific solutions.
Method 3: Using Substitution
If you have another equation involving x and y, you can use substitution to solve for both variables simultaneously. Let's assume we have a second equation:
x + y = 7
Steps:
-
Solve one equation for one variable: Let's solve the second equation for y: y = 7 - x
-
Substitute: Substitute this expression for y into the original equation (y = 2x + 5): 7 - x = 2x + 5
-
Solve for x: Now we have a single equation with only one variable (x). Solve for x:
- Add x to both sides: 7 = 3x + 5
- Subtract 5 from both sides: 2 = 3x
- Divide both sides by 3: x = 2/3
-
Solve for y: Substitute the value of x (2/3) back into either of the original equations to solve for y. Using y = 7 - x: y = 7 - (2/3) = 19/3
Therefore, the solution to the system of equations is x = 2/3 and y = 19/3.
Applications of y = 2x + 5
The equation y = 2x + 5, despite its simplicity, finds applications in various fields:
-
Modeling Linear Relationships: In many real-world scenarios, variables exhibit a linear relationship. For example, the total cost (y) of purchasing x items at $2 each with a $5 shipping fee can be modeled using this equation.
-
Physics: Equations of motion often involve linear relationships. This equation could represent the distance traveled (y) as a function of time (x) under constant acceleration.
-
Economics: Simple linear models in economics might use this equation to represent relationships between supply and demand, or cost and revenue.
-
Computer Science: This equation can be used in algorithms and simulations involving linear growth or relationships.
Expanding the Concept: Solving More Complex Equations
Understanding how to solve y = 2x + 5 provides a solid foundation for tackling more complex equations. The principles of isolating variables through inverse operations remain the same, even when dealing with higher-order polynomials, exponential functions, or systems of equations.
For instance, consider the equation 3y = 6x + 15. While seemingly different, it's simply a variation of the original equation. Dividing the entire equation by 3 reduces it back to y = 2x + 5.
Conclusion: Mastering the Fundamentals
The ability to solve the equation y = 2x + 5 is a fundamental skill in algebra. This seemingly simple equation teaches crucial concepts about variables, equations, and manipulation, laying the groundwork for more advanced mathematical concepts. By understanding the different approaches to solving for x, including algebraic manipulation, graphing, and substitution, you build a strong foundation for success in more complex mathematical endeavors. Remember, practice is key. The more you work with these types of equations, the more intuitive and effortless the process will become.
Latest Posts
Latest Posts
-
Write The Prime Factorization Of 18
May 11, 2025
-
Hcl Bond Type Polar Or Nonpolar
May 11, 2025
-
What Is Released Or Absorbed When Chemical Bonds Are Broken
May 11, 2025
-
Why Are Atoms Neutral Despite Having Charged Particles
May 11, 2025
-
What Is The Prime Factorization Of 112
May 11, 2025
Related Post
Thank you for visiting our website which covers about Y 2x 5 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.