Y 2x 4 6x 3y 12
listenit
May 13, 2025 · 5 min read
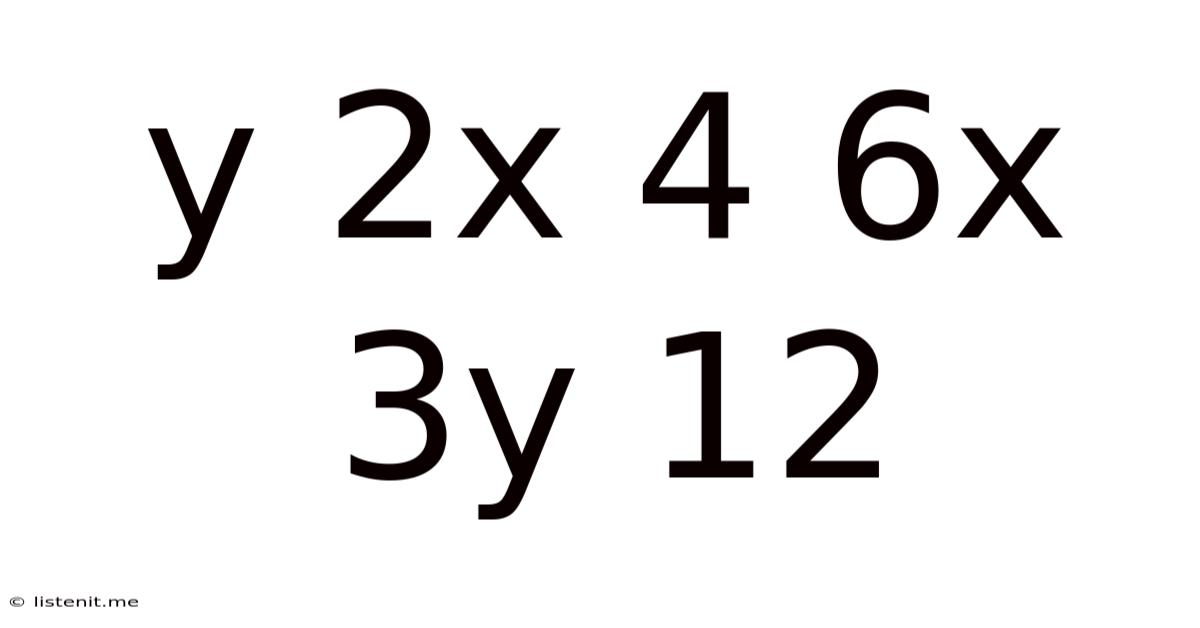
Table of Contents
Deconstructing the Mathematical Relationship: y = 2x, 4 = 6x - 3y, and 12
This article delves into the intricacies of the mathematical expressions y = 2x, 4 = 6x - 3y, and explores their interrelationships. We'll analyze each equation individually, explore methods for solving them, and investigate the geometric interpretations of these relationships. Understanding these concepts is fundamental to grasping various mathematical principles and applying them to real-world scenarios.
Understanding the Individual Equations
Let's break down each equation separately to gain a solid foundation before analyzing them together.
y = 2x: A Linear Equation
The equation y = 2x represents a simple linear relationship. This means that for every unit increase in 'x', 'y' increases by two units. This is a direct proportionality; 'y' is directly proportional to 'x' with a constant of proportionality equal to 2.
- Slope: The slope of this line is 2, indicating the steepness of the line on a graph. A positive slope signifies a positive correlation; as 'x' increases, 'y' also increases.
- Y-intercept: The y-intercept is 0, meaning the line passes through the origin (0,0) on the Cartesian coordinate system.
- Graphical Representation: This equation will be a straight line passing through the origin with a positive slope.
4 = 6x - 3y: A Linear Equation in Standard Form
The equation 4 = 6x - 3y is a linear equation presented in standard form (Ax + By = C). While it might appear more complex, it's fundamentally the same type of relationship as y = 2x. We can easily rearrange it to the slope-intercept form (y = mx + b) to better understand its characteristics.
Let's rearrange the equation:
- Add 3y to both sides: 3y + 4 = 6x
- Subtract 4 from both sides: 3y = 6x - 4
- Divide both sides by 3: y = 2x - 4/3
Now, we can clearly see the characteristics:
- Slope: The slope is still 2, indicating the same rate of change as in the first equation.
- Y-intercept: The y-intercept is -4/3, meaning the line intersects the y-axis at the point (0, -4/3).
- Graphical Representation: This equation represents a parallel line to y = 2x, shifted downwards by 4/3 units.
Solving the System of Equations
Since we have two linear equations, we can solve for the values of 'x' and 'y' that satisfy both equations simultaneously. There are several methods to achieve this:
1. Substitution Method
We can substitute the expression for 'y' from the first equation (y = 2x) into the second equation:
4 = 6x - 3(2x)
Simplifying this equation:
4 = 6x - 6x 4 = 0
This result indicates that there is no solution to this system of equations. The two lines are parallel and will never intersect.
2. Elimination Method
The elimination method involves manipulating the equations to eliminate one variable and solve for the other. Let's try this approach:
First, let's rewrite the equations:
y = 2x 6x - 3y = 4
We can multiply the first equation by 3 to get:
3y = 6x
Now, subtract this equation from the second equation:
(6x - 3y) - (6x) = 4 - 0
This simplifies to:
-3y = 4 y = -4/3
Now, substitute this value of 'y' back into the first equation:
-4/3 = 2x x = -2/3
However, if we substitute x = -2/3 and y = -4/3 into the second equation, we get:
6(-2/3) - 3(-4/3) = -4 + 4 = 0 ≠ 4
This again confirms that there's no solution that satisfies both equations simultaneously. The inconsistency highlights the parallel nature of the lines.
Geometric Interpretation and Analysis of Parallel Lines
The fact that we find no solution graphically translates to parallel lines. Both lines have the same slope (2), indicating they are parallel and will never intersect. Therefore, there is no point (x, y) that satisfies both equations simultaneously. This is a crucial concept in linear algebra and geometry.
Expanding the Problem: Adding a Third Equation (12)
The introduction of "12" as a separate element requires clarification. It's not immediately clear how this number relates to the previous two equations. It could represent:
- A constant: Perhaps it's an additional constraint or a value related to a specific application of the equations. Without further context, we can't definitively determine its role.
- A separate equation: It could be part of a larger system of equations. For example, it could represent a constraint like z = 12, where 'z' is a third variable. This would require additional equations to solve the system fully.
- A constraint on the solution space: If the context suggests a range or domain for the variables x and y, then 12 might be the upper limit of one or both variables. This would also require further context or constraints.
Therefore, the inclusion of "12" without specifying its relationship to the other equations renders it an independent element that cannot be directly incorporated into the solution of the initial system.
Real-World Applications and Extensions
Understanding systems of linear equations is critical in numerous fields:
- Economics: Supply and demand curves, linear programming problems.
- Physics: Modeling motion, calculating forces and velocities.
- Engineering: Structural analysis, circuit design.
- Computer Science: Linear algebra is fundamental to computer graphics, machine learning, and many other areas.
This seemingly simple problem involving the equations y = 2x, 4 = 6x - 3y, and the additional element "12" illustrates important concepts about solving systems of equations, analyzing linear relationships, and interpreting geometrical representations. The lack of a solution emphasizes the significance of understanding the implications of parallel lines and the importance of clear and complete problem statements. Further context is needed to meaningfully incorporate the number 12 into this analysis.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about Y 2x 4 6x 3y 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.