Y 2 1 2 X 2
listenit
May 11, 2025 · 5 min read
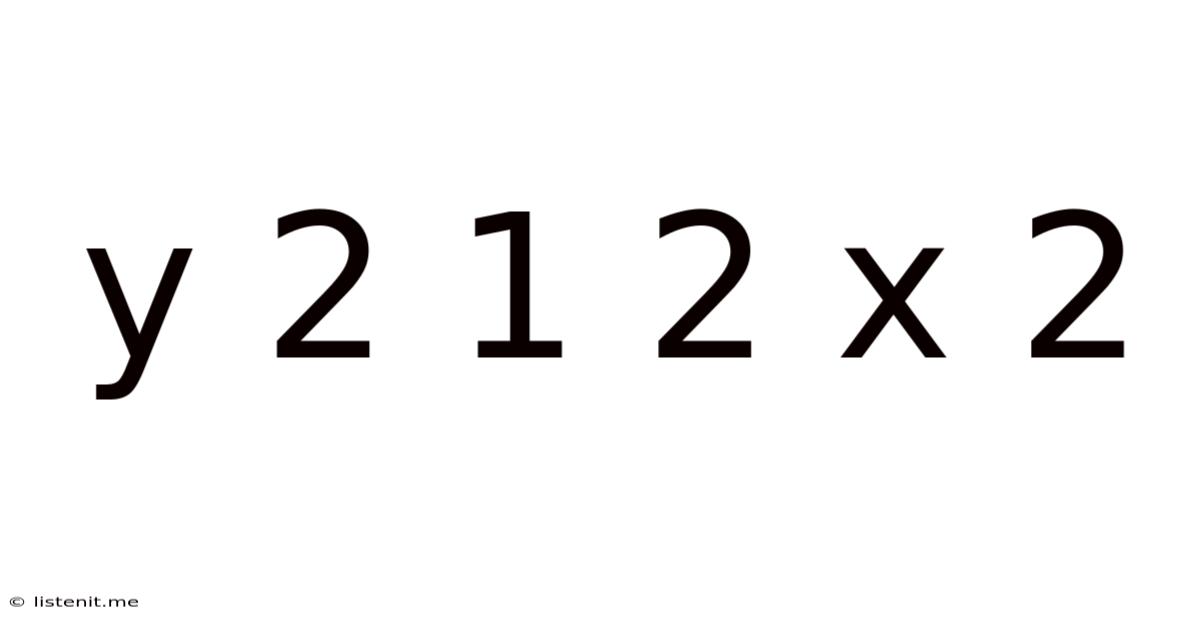
Table of Contents
Decoding the Enigma: A Deep Dive into Y = 2 / (1 + 2x²)
The seemingly simple equation, Y = 2 / (1 + 2x²), hides a surprising depth of mathematical richness. While its basic form might appear straightforward, exploring its properties reveals fascinating insights into function behavior, calculus applications, and even potential real-world applications. This article will delve into a comprehensive analysis of this equation, examining its characteristics, graphing techniques, derivative analysis, integral calculations, and potential applications.
Understanding the Basic Structure
At its core, Y = 2 / (1 + 2x²) represents a rational function. This means it's a ratio of two polynomial functions: a constant numerator (2) and a quadratic denominator (1 + 2x²). This particular structure leads to several key features that shape its behavior.
Key Characteristics:
-
Even Function: The equation demonstrates even symmetry. This means that f(x) = f(-x). Graphically, this translates to symmetry about the y-axis. Substituting -x for x results in the same output value, highlighting this inherent symmetry.
-
Horizontal Asymptote: As x approaches positive or negative infinity, the term 2x² dominates the denominator. Consequently, the function approaches zero. This establishes a horizontal asymptote at Y = 0. The function will never actually reach zero, always approaching it asymptotically.
-
No Vertical Asymptotes: The denominator (1 + 2x²) is always positive, regardless of the value of x. This is because squaring a real number always results in a non-negative value, ensuring that the denominator never equals zero. The absence of vertical asymptotes signifies the function's continuous nature across the entire real number line.
Graphing the Function: A Visual Representation
Visualizing the function is crucial for understanding its behavior. Several techniques can be used to graph Y = 2 / (1 + 2x²):
Manual Plotting:
Creating a graph manually involves selecting various x-values, calculating the corresponding y-values, and plotting the points on a coordinate plane. It's a laborious process, but it helps build an intuitive understanding of the function's shape. Points of interest include x=0 (where Y=2, representing the maximum value of the function), and values as x approaches positive and negative infinity (approaching the asymptote at Y=0).
Utilizing Graphing Software:
Software like Desmos, GeoGebra, or MATLAB provides a much more efficient way to graph the function. Inputting the equation directly will generate a precise graph, showcasing the function's symmetry, maximum value, and asymptotic behavior with ease. This allows for quicker analysis and exploration of the function's characteristics.
Key Features to Observe on the Graph:
-
Maximum Value: The graph clearly shows that the maximum value occurs at x = 0, where Y = 2. This point represents the peak of the curve.
-
Symmetry: The graph visually demonstrates the even symmetry, with a perfect mirror image reflected about the y-axis.
-
Asymptotic Behavior: The graph clearly approaches the horizontal asymptote at Y = 0 as x tends towards positive and negative infinity.
Calculus Applications: Exploring Derivatives and Integrals
Applying calculus allows us to delve deeper into the function's behavior. Calculating the derivative provides insights into its slope at any given point, while calculating the integral unveils the area under its curve.
The Derivative: Unveiling the Slope
The derivative, dy/dx, reveals the instantaneous rate of change of the function. Using the quotient rule, we find the derivative of Y = 2 / (1 + 2x²) to be:
dy/dx = -8x / (1 + 2x²)²
This derivative highlights several crucial points:
-
Critical Point: The derivative equals zero when x = 0. This confirms the maximum value at x = 0, as the slope is zero at this point (a stationary point).
-
Increasing and Decreasing Intervals: The derivative is positive for x < 0 and negative for x > 0. This indicates that the function is increasing on the interval (-∞, 0) and decreasing on the interval (0, ∞).
The Integral: Calculating the Area Under the Curve
Calculating the definite integral of the function provides the area under the curve between two specified x-values. Finding the indefinite integral, however, is more challenging and might involve trigonometric substitution or other advanced integration techniques. While an exact solution might be complex, numerical methods can readily approximate the definite integral over a given interval. This provides valuable insights into the accumulated area under the curve.
Potential Applications: A Glimpse into Real-World Relevance
While the equation might seem abstract, it can find applications in various fields, often as a component within more complex models:
Probability and Statistics:
Functions similar to this are sometimes used to model probability density functions (PDFs). Specifically, the Gaussian function (normal distribution) has a similar bell shape and asymptotic behavior. Understanding this equation can help build an intuition for similar probability distributions.
Physics and Engineering:
In physics and engineering, functions of this type might appear in models related to damped oscillations or wave phenomena. The asymptotic behavior could represent the decay of an oscillatory system over time.
Computer Graphics and Modeling:
The function's smooth, symmetric nature could be used to create various curves or shapes in computer graphics or modeling applications. Modifying the parameters (e.g., changing the coefficients in the denominator) can alter the curve's shape, enabling diverse graphical elements.
Economics and Finance:
In economics and finance, functions of this form may arise in models describing utility functions or risk aversion. The shape of the curve could relate to diminishing marginal utility, where the increase in utility from an additional unit decreases as the quantity increases.
Conclusion: A Rich Mathematical Landscape
The equation Y = 2 / (1 + 2x²) is a seemingly simple expression that reveals a surprising depth of mathematical complexity. Through analysis of its basic structure, graphical representation, calculus applications, and potential real-world relevance, we have explored the rich landscape hidden within this seemingly simple equation. Its symmetrical nature, asymptotic behavior, and the insights derived from its derivatives and integrals provide a fertile ground for further mathematical exploration and practical application across numerous fields. Understanding this function offers a valuable stepping stone towards mastering more complex mathematical concepts and models. Further exploration could involve analyzing different transformations of this function, exploring its behavior in higher dimensions, or investigating related functions that share similar properties. The possibilities are vast and invite further investigation by curious minds.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about Y 2 1 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.