X 3 7x 12 2 3
listenit
May 24, 2025 · 5 min read
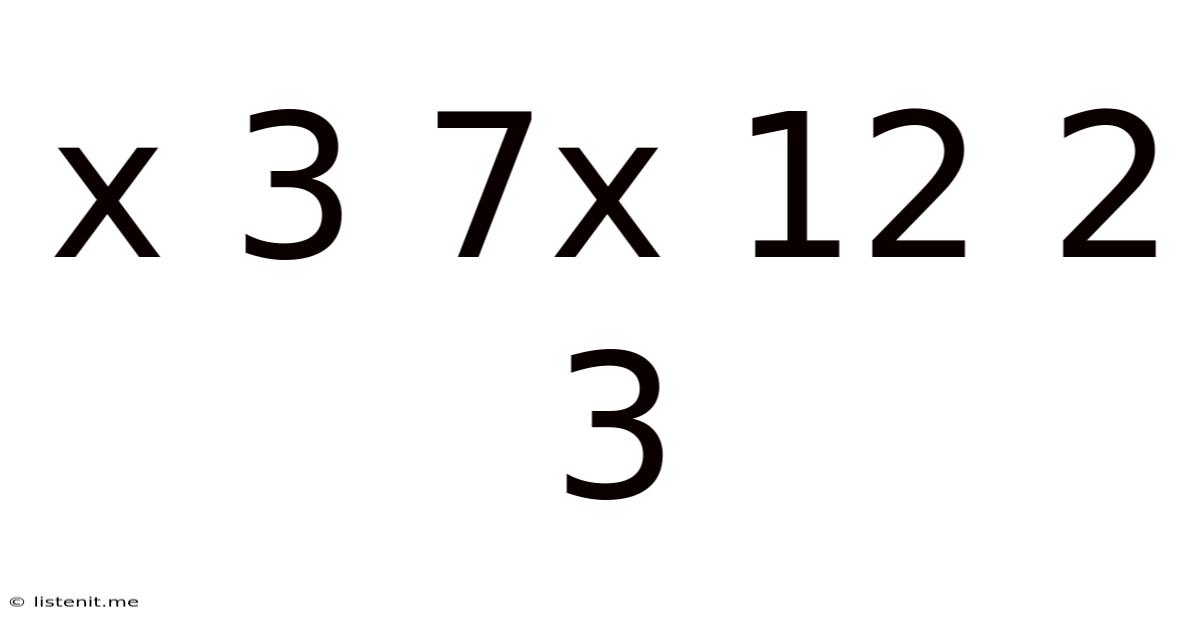
Table of Contents
Decoding the Mathematical Expression: x³ + 7x² + 12x + 2/3
This article delves into the mathematical expression x³ + 7x² + 12x + 2/3, exploring its various aspects, from basic algebraic manipulation to advanced techniques like solving for roots and understanding its graphical representation. We'll cover topics that are crucial for students and professionals alike, aiming to provide a comprehensive understanding of this seemingly simple yet surprisingly rich polynomial.
Understanding Cubic Polynomials
Before we dive into the specifics of x³ + 7x² + 12x + 2/3, let's establish a foundation in understanding cubic polynomials. A cubic polynomial is a polynomial of degree three, meaning the highest power of the variable (in this case, x) is three. The general form of a cubic polynomial is ax³ + bx² + cx + d, where a, b, c, and d are constants, and 'a' is not equal to zero (otherwise it wouldn't be a cubic polynomial).
Our expression, x³ + 7x² + 12x + 2/3, fits this general form perfectly, with a = 1, b = 7, c = 12, and d = 2/3. Understanding this general form is vital for applying various mathematical techniques.
Analyzing the Coefficients
The coefficients (1, 7, 12, and 2/3) hold significant information about the behavior of the polynomial. While a full analysis requires advanced techniques, we can make some preliminary observations:
-
The leading coefficient (a = 1): A positive leading coefficient indicates that the polynomial will increase towards positive infinity as x approaches positive infinity and decrease towards negative infinity as x approaches negative infinity. This gives us a general idea of the overall shape of the curve.
-
The constant term (d = 2/3): This is the y-intercept of the polynomial. When x = 0, the polynomial evaluates to 2/3.
-
The remaining coefficients (b = 7 and c = 12): These coefficients influence the shape of the curve, particularly the location and nature of its turning points (local maxima and minima). A more detailed analysis would require calculus techniques.
Finding the Roots (Zeros) of the Polynomial
Finding the roots (or zeros) of a polynomial means finding the values of x for which the polynomial evaluates to zero. This is often a challenging task, especially for cubic polynomials. There's no single, universally applicable formula like the quadratic formula for solving cubic equations. However, several methods exist:
-
Rational Root Theorem: This theorem helps identify potential rational roots (roots that are fractions of integers). It states that any rational root p/q (where p and q are integers and q ≠ 0) must have 'p' as a factor of the constant term (2/3 in our case) and 'q' as a factor of the leading coefficient (1 in our case). This narrows down the possibilities, but doesn't guarantee finding all roots.
-
Numerical Methods: For cubic polynomials that don't have easily identifiable rational roots, numerical methods like the Newton-Raphson method or the bisection method are employed. These iterative methods provide increasingly accurate approximations of the roots.
-
Graphical Method: Plotting the polynomial using graphing software or a calculator provides a visual representation of the polynomial and allows for approximating the roots by observing where the graph intersects the x-axis.
Graphing the Polynomial
The graphical representation of x³ + 7x² + 12x + 2/3 is crucial for understanding its behavior. The graph will be a continuous curve, with the general shape determined by the positive leading coefficient (as mentioned earlier). The graph will intersect the y-axis at (0, 2/3). The exact shape, including the location of turning points and the x-intercepts (roots), can be determined using graphing software or by plotting points after calculating their corresponding y-values.
Applications of Cubic Polynomials
Cubic polynomials have wide-ranging applications across various fields:
-
Engineering: Cubic functions are used to model the shape of curves in engineering designs, such as the path of a projectile or the shape of a roller coaster track.
-
Physics: Cubic equations can describe the motion of objects under certain conditions, and are relevant in areas like fluid dynamics.
-
Economics: Cubic functions can be used to model cost functions or production functions in economic models.
-
Computer Graphics: Cubic curves (like Bézier curves) are widely used in computer graphics for creating smooth, curved lines and surfaces.
Advanced Techniques: Calculus and Differentiation
To gain a deeper understanding of the polynomial's behavior, we can utilize calculus. Taking the derivative of the polynomial provides information about its slope at any given point:
The derivative of x³ + 7x² + 12x + 2/3 is 3x² + 14x + 12.
Setting the derivative equal to zero and solving the resulting quadratic equation (3x² + 14x + 12 = 0) gives us the x-coordinates of the turning points (local maxima and minima) of the original cubic polynomial.
Conclusion
The seemingly simple mathematical expression x³ + 7x² + 12x + 2/3 opens up a world of mathematical exploration. From basic algebraic manipulation to advanced techniques like finding roots, graphing, and employing calculus, this polynomial showcases the richness and complexity embedded within seemingly straightforward equations. Understanding cubic polynomials and the various methods for analyzing them is vital in many fields, highlighting their importance in both theoretical and applied mathematics. Further exploration using specialized software and numerical techniques can provide even more precise insights into the behavior and applications of this fascinating polynomial. This detailed analysis, combining theoretical concepts with practical applications, ensures a comprehensive understanding for both beginners and advanced learners. The exploration of this polynomial provides a solid foundation for tackling more complex mathematical challenges in the future. Remember to always approach mathematical problems systematically, breaking them down into smaller, manageable steps to facilitate a deeper comprehension.
Latest Posts
Latest Posts
-
What Is My Mortgage Payoff Amount
May 25, 2025
-
If Born In 1962 How Old Are You
May 25, 2025
-
Mortgage On A 4 Million Dollar Home
May 25, 2025
-
3 Out Of 19 As A Percentage
May 25, 2025
-
What Btu Heater Do I Need
May 25, 2025
Related Post
Thank you for visiting our website which covers about X 3 7x 12 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.