X 3 3x 2 4x 12
listenit
Mar 21, 2025 · 5 min read
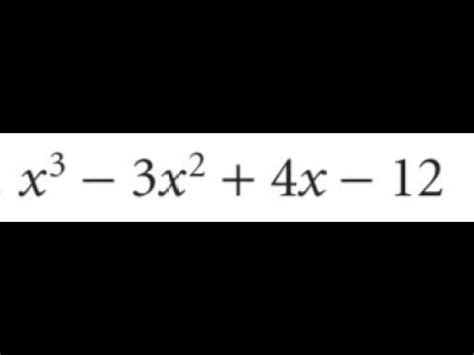
Table of Contents
- X 3 3x 2 4x 12
- Table of Contents
- Deconstructing the Mathematical Expression: x³ + 3x² + 4x + 12
- Factoring the Expression: Unveiling the Hidden Structure
- 1. The Grouping Method: A Strategic Approach
- 2. Exploring the Quadratic Factor: Complex Numbers
- Graphical Representation: Visualizing the Expression
- 1. Identifying Key Features: Roots and Intercepts
- 2. Sketching the Curve: Behavior and Turning Points
- Applications and Real-World Connections
- 1. Modeling Physical Phenomena: Volume and Motion
- 2. Engineering and Design: Optimization Problems
- 3. Data Analysis and Modeling: Curve Fitting
- Further Exploration: Beyond the Basics
- Conclusion: A Deeper Appreciation of Algebraic Structures
- Latest Posts
- Latest Posts
- Related Post
Deconstructing the Mathematical Expression: x³ + 3x² + 4x + 12
The seemingly simple algebraic expression, x³ + 3x² + 4x + 12, presents a fascinating opportunity to delve into the world of mathematics. This article will explore various aspects of this expression, from its basic factorization to its graphical representation and applications in real-world scenarios. We'll analyze its properties, explore different methods of solving related problems, and uncover the underlying mathematical concepts that give it meaning. By the end, you'll have a much deeper understanding not only of this specific expression but also of broader algebraic principles.
Factoring the Expression: Unveiling the Hidden Structure
The primary challenge with this cubic expression is finding its factors. Unlike simpler quadratic expressions, there isn't a readily apparent formula for directly factoring a cubic. However, we can employ several techniques to uncover the hidden structure.
1. The Grouping Method: A Strategic Approach
One common approach is the grouping method. We look for common factors within groups of terms:
x³ + 3x² + 4x + 12
We can group the terms as follows:
(x³ + 3x²) + (4x + 12)
Now, we factor out the greatest common factor (GCF) from each group:
x²(x + 3) + 4(x + 3)
Notice that both terms now share a common factor of (x + 3). We can factor this out:
(x + 3)(x² + 4)
This gives us the factored form of the expression. We now have two factors: (x + 3) and (x² + 4).
2. Exploring the Quadratic Factor: Complex Numbers
The quadratic factor (x² + 4) is interesting. While it doesn't factor further using real numbers, we can factor it using complex numbers. Recall that i represents the imaginary unit, where i² = -1.
We can rewrite (x² + 4) as (x² - (-4)). This allows us to use the difference of squares factorization:
x² - (-4) = x² - (2i)² = (x - 2i)(x + 2i)
Therefore, the complete factorization using complex numbers is:
(x + 3)(x - 2i)(x + 2i)
This demonstrates how extending our number system to include complex numbers allows us to fully factor even seemingly irreducible polynomials.
Graphical Representation: Visualizing the Expression
Understanding the graphical representation of x³ + 3x² + 4x + 12 provides valuable insight into its behavior. Plotting this cubic function reveals its shape, intercepts, and other key characteristics.
1. Identifying Key Features: Roots and Intercepts
The x-intercept(s) are the points where the graph crosses the x-axis (where y = 0). These correspond to the roots or zeros of the polynomial. From our factorization, we know one real root is x = -3. The complex roots, x = 2i and x = -2i, do not appear on the real x-axis.
The y-intercept is the point where the graph crosses the y-axis (where x = 0). By substituting x = 0 into the expression, we find the y-intercept is 12.
2. Sketching the Curve: Behavior and Turning Points
The cubic function will have a general "S" shape. Because the coefficient of the x³ term is positive (1), the graph will rise to the right and fall to the left. The presence of the real root at x = -3 and the positive y-intercept indicates that the graph will pass through (-3, 0) and (0, 12).
Determining the precise location of turning points requires calculus (finding the derivative and setting it to zero), but a general sketch can be made based on the known information.
Applications and Real-World Connections
While seemingly abstract, cubic polynomials and similar expressions find numerous applications in various fields:
1. Modeling Physical Phenomena: Volume and Motion
Cubic functions can effectively model the volume of a three-dimensional object as a function of one of its dimensions. For example, the volume of a cube is given by V = x³, and slightly more complex shapes can lead to cubic polynomial expressions. In physics, cubic equations can describe certain types of motion or relationships between variables.
2. Engineering and Design: Optimization Problems
Engineers frequently encounter cubic equations when optimizing designs. Finding the maximum volume of a container subject to constraints, or the optimal dimensions for structural elements, often involves solving cubic equations.
3. Data Analysis and Modeling: Curve Fitting
In statistical analysis, cubic functions can be used to fit curves to data points. This is useful when a linear relationship doesn't adequately capture the trends in the data. The cubic equation provides a more flexible model to capture the complexities in the observed data.
Further Exploration: Beyond the Basics
The exploration of x³ + 3x² + 4x + 12 can extend far beyond what's been discussed:
- Numerical Methods: If factoring isn't straightforward, numerical methods (like the Newton-Raphson method) can approximate the roots of the cubic equation.
- Calculus: Applying calculus provides a deeper understanding of the function's behavior—its rate of change, turning points, and concavity.
- Polynomial Division: Polynomial long division can be used to verify the factorization or explore other relationships between polynomials.
Conclusion: A Deeper Appreciation of Algebraic Structures
This in-depth exploration of the seemingly simple expression x³ + 3x² + 4x + 12 reveals a rich mathematical landscape. From its factorization and graphical representation to its applications in various fields, this expression serves as a microcosm of fundamental algebraic concepts. By understanding its properties and exploring the related techniques, we develop a stronger foundation for tackling more complex mathematical challenges. The journey from a simple equation to a comprehensive understanding highlights the elegance and power of mathematics in solving real-world problems and uncovering hidden structures within seemingly straightforward expressions. The seemingly simple equation opens doors to a vast world of mathematical exploration and applications.
Latest Posts
Latest Posts
-
Why Is Plastic A Good Insulator
Mar 28, 2025
-
1000 Ml Equals How Many Liters
Mar 28, 2025
-
Inverse Of X 2 X 1
Mar 28, 2025
-
What Is The Mass Number Of Magnesium
Mar 28, 2025
-
How Many Symmetrical Lines Does A Rectangle Have
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 4x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
