X 2 Y 2 Z 2 Z
listenit
May 09, 2025 · 5 min read
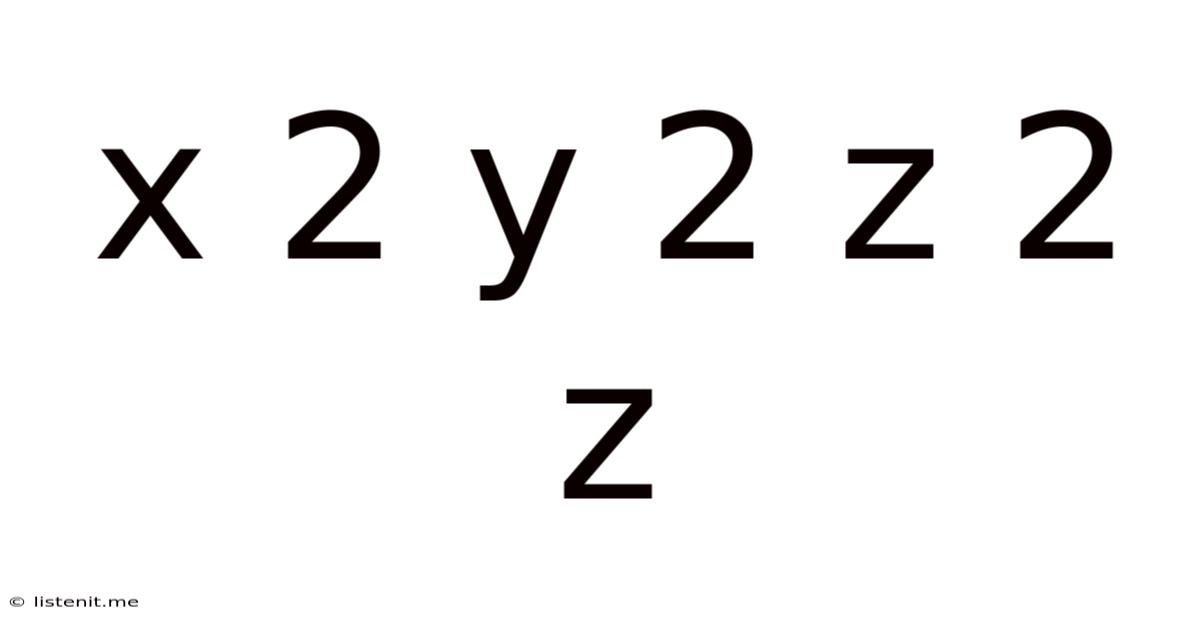
Table of Contents
Exploring the Mathematical Landscape of x² + y² + z² = z
The equation x² + y² + z² = z presents a fascinating challenge in mathematics, blending elements of algebra, geometry, and number theory. This seemingly simple equation hides a rich tapestry of solutions and interpretations, inviting us to explore its properties and delve into the mathematical concepts it embodies. This article will embark on a comprehensive exploration of this equation, examining its solutions, geometric interpretations, and connections to broader mathematical fields.
Understanding the Equation's Structure
At first glance, x² + y² + z² = z might appear straightforward. However, its simplicity belies its complexity. The equation represents a quadratic relationship between three variables, x, y, and z. Unlike a linear equation, which produces a straight line in two dimensions, this equation describes a three-dimensional surface. Understanding its structure requires examining its individual components and their interrelationships.
The Quadratic Terms: x², y², and z²
The squared terms, x², y², and z², introduce a non-linearity to the equation. This non-linearity is crucial because it leads to a curved surface rather than a flat plane. The squares ensure that both positive and negative values of x, y, and z contribute positively to the sum, preventing simple cancellation effects.
The Linear Term: z
The presence of the linear term, z, on the right-hand side fundamentally alters the equation's behavior. It introduces an asymmetry, meaning the equation isn't symmetric with respect to z. This asymmetry has significant implications for the types of solutions we can expect. It's no longer a purely symmetric quadratic form.
Finding Solutions: An Analytical Approach
Solving x² + y² + z² = z analytically requires careful consideration of the equation's structure. One approach involves rearranging the equation to isolate z:
z² - z + (x² + y²) = 0
This is a quadratic equation in z. We can use the quadratic formula to solve for z:
z = [1 ± √(1 - 4(x² + y²))] / 2
This formula reveals several important aspects of the equation's solutions:
Real Solutions: The Discriminant
The expression inside the square root, 1 - 4(x² + y²), is the discriminant. For real solutions to exist, the discriminant must be non-negative:
1 - 4(x² + y²) ≥ 0
This inequality places a constraint on the possible values of x and y:
x² + y² ≤ 1/4
This inequality defines a disk in the xy-plane with a radius of 1/2 centered at the origin. This means that real solutions for z only exist when x and y are within this disk. Outside this disk, the solutions for z become complex numbers.
Complex Solutions: Extending Beyond Reality
When the discriminant is negative, the solutions for z become complex numbers. This signifies that the equation extends beyond the realm of real numbers into the complex plane, adding another layer of richness to its mathematical properties. Exploring these complex solutions requires delving into the properties of complex numbers and their geometric representation.
Geometric Interpretation: Visualizing the Equation
The equation x² + y² + z² = z can be visualized as a three-dimensional surface. To understand its shape, we can rewrite the equation as:
x² + y² + (z - 1/2)² = 1/4
This equation represents a sphere with a radius of 1/2 centered at (0, 0, 1/2). This geometric interpretation provides valuable insights into the nature of the solutions and their distribution in three-dimensional space.
The Sphere's Properties: Radius and Center
The sphere's radius of 1/2 directly relates to the constraint on x and y we derived earlier. The center of the sphere, (0, 0, 1/2), reflects the asymmetry introduced by the linear term z. This asymmetry is visually evident in the sphere's position, not being centered at the origin.
Connections to Other Mathematical Fields
The equation x² + y² + z² = z connects to several other mathematical fields, broadening its significance and offering avenues for further exploration.
Number Theory: Integer Solutions
A natural question arising from the equation is whether integer solutions exist. Exploring this question requires delving into number theory and Diophantine equations, which deal with equations where solutions are restricted to integers. Finding integer solutions for this specific equation would involve systematically testing integer values of x, y, and z, potentially using computational methods.
Linear Algebra: Systems of Equations
The equation can be viewed as a single equation within a larger system of equations. Combining it with other equations can lead to systems of equations that may have unique solutions or families of solutions, depending on the nature of the additional equations.
Calculus: Optimization Problems
The equation could be used in optimization problems within calculus. For example, finding the minimum or maximum values of a function subject to the constraint given by the equation would require the techniques of constrained optimization.
Exploring Variations and Extensions
The simplicity of x² + y² + z² = z allows for numerous variations and extensions, creating opportunities for further mathematical exploration:
Variations in Coefficients
Introducing coefficients to the variables would alter the equation's properties significantly. For example, ax² + by² + cz² = dz would present a different geometrical representation and a different set of solutions. The analysis would become more involved, requiring a deeper examination of the influence of each coefficient on the equation's behavior.
Higher Dimensions: Generalizing the Equation
The concept can be extended to higher dimensions. For example, in four dimensions, the equation could be written as x² + y² + z² + w² = w. The geometric interpretation would become more challenging, but the analytical approach using similar techniques could still be applied. Exploring higher dimensional generalizations opens doors to a wealth of abstract mathematical concepts.
Applications in Physics and Engineering
While primarily a mathematical exploration, equations with similar forms frequently appear in physics and engineering. They may represent physical systems or phenomena, offering a potential connection between theoretical mathematics and practical applications.
Conclusion: A Rich Field for Exploration
The equation x² + y² + z² = z, despite its apparent simplicity, unveils a rich and multifaceted landscape for mathematical exploration. Its solutions, geometric interpretation, and connections to other mathematical fields provide a compelling case study for understanding the interplay between algebra, geometry, and number theory. From its real and complex solutions to its potential applications in optimization and other fields, this seemingly simple equation offers endless possibilities for deeper inquiry and reveals the power of mathematics to unveil hidden complexity within apparently simple structures. Furthermore, exploring variations and extensions of the equation paves the way for discoveries in higher dimensions and potential applications in diverse fields, highlighting the importance of even the most basic mathematical equations in advancing our understanding of the world around us.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 12 And 60
May 09, 2025
-
How To Find An Equation Of A Line Parallel
May 09, 2025
-
How Many Real Solutions Does The System Of Equations Have
May 09, 2025
-
What Percent Of 80 Is 65
May 09, 2025
-
Protein Polymers Are Made Up Of
May 09, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z 2 Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.