X 2 Y 2 X 2
listenit
May 09, 2025 · 4 min read
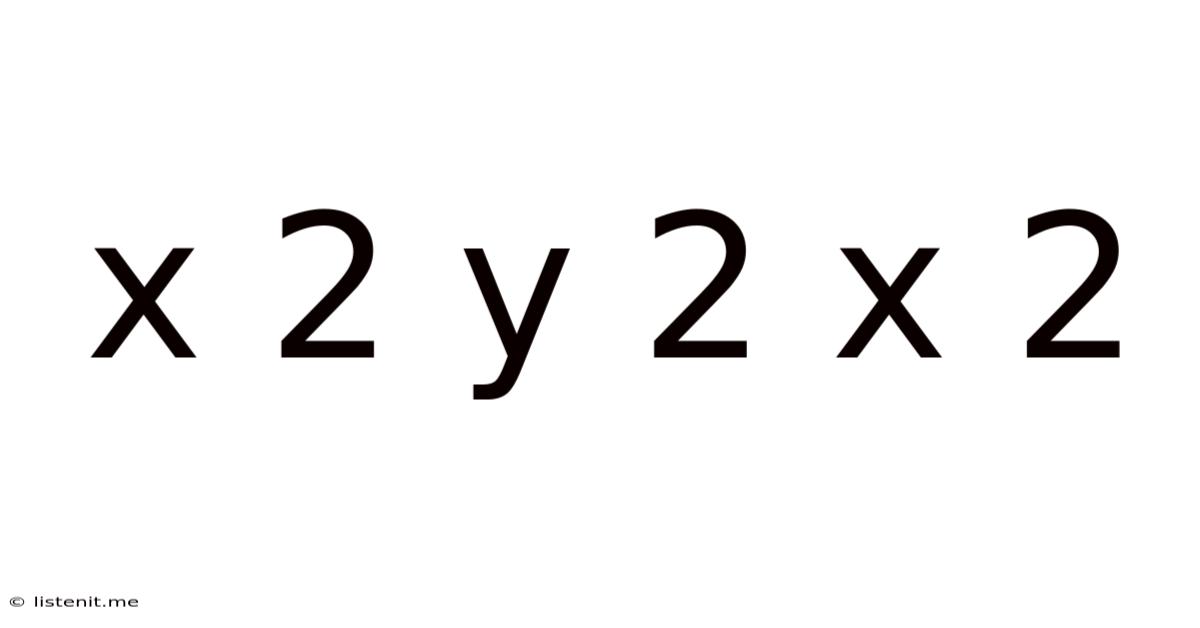
Table of Contents
Decoding the Enigma: A Deep Dive into x² + y² = z² and its Implications
The equation x² + y² = z² might seem deceptively simple at first glance. This seemingly innocuous algebraic expression, however, unlocks a world of mathematical exploration, touching upon geometry, number theory, and even cryptography. This article will delve into the intricacies of this equation, exploring its solutions, its geometric representation, and its far-reaching implications across various mathematical disciplines.
Understanding the Fundamentals: Pythagorean Triples
At its core, x² + y² = z² represents the Pythagorean theorem, a cornerstone of Euclidean geometry. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Solutions to x² + y² = z², where x, y, and z are integers, are known as Pythagorean triples.
Examples of Pythagorean Triples
Some well-known examples of Pythagorean triples include:
- (3, 4, 5): 3² + 4² = 9 + 16 = 25 = 5²
- (5, 12, 13): 5² + 12² = 25 + 144 = 169 = 13²
- (8, 15, 17): 8² + 15² = 64 + 225 = 289 = 17²
These triples represent the lengths of the sides of right-angled triangles with integer side lengths. Finding all possible Pythagorean triples forms a significant part of the study of number theory.
Generating Pythagorean Triples: Euclid's Formula
Fortunately, we don't need to rely solely on trial and error to find Pythagorean triples. Euclid's formula provides a systematic method for generating them. Given two integers, m and n, where m > n > 0, the following equations generate a Pythagorean triple:
- x = m² - n²
- y = 2mn
- z = m² + n²
By varying the values of m and n, we can generate an infinite number of Pythagorean triples. For instance, if we let m = 2 and n = 1, we obtain the triple (3, 4, 5). If we let m = 3 and n = 2, we get (5, 12, 13), and so on.
The Significance of Euclid's Formula
Euclid's formula is significant because it demonstrates that there are infinitely many Pythagorean triples. This is a crucial result in number theory, highlighting the richness and complexity of integer solutions to seemingly simple equations.
Beyond Integers: Exploring Rational and Real Solutions
The equation x² + y² = z² is not limited to integer solutions. It can also be extended to encompass rational and real numbers. In the realm of rational numbers (fractions), finding solutions involves finding sets of rational numbers that satisfy the equation. This opens up further avenues of mathematical exploration.
Geometric Interpretation: Circles and Spheres
Geometrically, the equation x² + y² = z² represents a circle in two dimensions (when z is considered a constant) and a sphere in three dimensions. This connection between algebra and geometry provides a powerful visual aid for understanding the equation's solutions. Visualizing these shapes allows for a deeper grasp of the relationships between x, y, and z.
Applications and Implications: A Wider Perspective
The seemingly simple equation x² + y² = z² extends far beyond its fundamental mathematical implications. It plays a significant role in various fields, including:
1. Cryptography
Pythagorean triples and their variations are used in certain cryptographic algorithms to create secure systems. The inherent difficulty in finding large Pythagorean triples contributes to the security of these systems.
2. Computer Graphics
The equation is fundamental in computer graphics for representing points in space and performing various geometrical calculations. Understanding the relationship between x, y, and z is crucial in creating realistic three-dimensional images and simulations.
3. Physics
Pythagorean triples and the Pythagorean theorem appear in various physics applications, such as calculating distances and velocities in three-dimensional space. Its relevance extends to areas such as classical mechanics and relativity.
4. Engineering
In engineering, the equation is essential for calculating distances, forces, and stresses in structural designs. The concept of right-angled triangles and their relationships are key in various engineering disciplines.
Advanced Exploration: Fermat's Last Theorem and Beyond
While x² + y² = z² has an abundance of solutions, Fermat's Last Theorem famously states that there are no whole number solutions to the equation xⁿ + yⁿ = zⁿ for any integer value of n greater than 2. This theorem, proven by Andrew Wiles in 1994, stands as a testament to the profound depth and complexity hidden within seemingly straightforward mathematical expressions. The quest to prove Fermat's Last Theorem spurred significant advancements in number theory.
Conclusion: The Enduring Legacy of x² + y² = z²
The equation x² + y² = z², while simple in appearance, holds a remarkable depth and breadth of mathematical significance. From its foundation as the Pythagorean theorem to its applications in diverse fields, this equation continues to inspire mathematical inquiry and innovation. Its exploration unveils the interconnectedness of various mathematical branches, highlighting the power and beauty of mathematics as a whole. Further research into generalizations and variations of this equation continues to push the boundaries of mathematical understanding, demonstrating its enduring legacy in the world of numbers and shapes. The seemingly simple equation x² + y² = z² offers a compelling journey into the heart of mathematics, revealing a richness and complexity that far exceeds initial expectations. Its impact extends beyond theoretical mathematics, finding practical application in various fields and serving as a testament to the enduring power of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Whats The Width Of A 70 Inch Tv
May 09, 2025
-
Find 3 Different Ratios That Are Equivalent To 7 3
May 09, 2025
-
Is Y 2x 3 A Function
May 09, 2025
-
What Is The Lowest Energy Level That Contains D Orbitals
May 09, 2025
-
How Many Neutrons In Oxygen 16
May 09, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.