X 2 X 2 X 2 X 2
listenit
Jun 14, 2025 · 6 min read
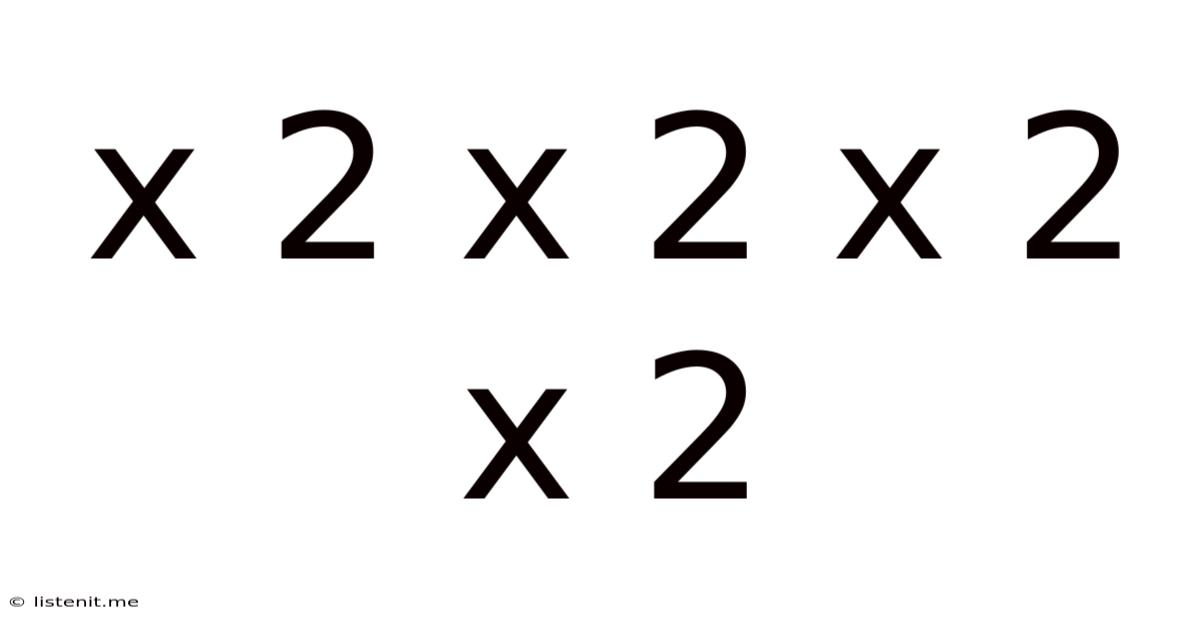
Table of Contents
Exploring the Mathematical and Conceptual Depths of 2 x 2 x 2 x 2: A Deep Dive into Exponential Growth and Beyond
The seemingly simple equation, 2 x 2 x 2 x 2, holds a surprising depth of meaning across various fields, from basic arithmetic to complex scientific principles. While the answer itself is straightforward (16), the process and implications of repeated multiplication, or exponentiation, reveal fascinating insights into exponential growth, geometric progression, and even the underlying structure of our universe. This article will embark on an exploration of this seemingly simple equation, uncovering its profound significance across diverse disciplines.
The Fundamentals: Arithmetic and Exponential Growth
At its core, 2 x 2 x 2 x 2 is a basic arithmetic problem. Elementary school students learn to solve this through repeated multiplication:
- 2 x 2 = 4
- 4 x 2 = 8
- 8 x 2 = 16
This simple calculation demonstrates the principle of exponential growth. Each successive multiplication by 2 results in a larger increase than the previous one. This contrasts with linear growth, where the increase remains constant. For instance, adding 2 repeatedly (2 + 2 + 2 + 2 = 8) demonstrates linear growth – a constant rate of change. Exponential growth, however, exhibits an accelerating rate of change.
This difference becomes strikingly apparent when considering the implications over longer periods. Imagine starting with a single bacterium that doubles every hour. After four hours, you'd have 16 bacteria (2 x 2 x 2 x 2). However, after 24 hours (one day), you'd have over 16 million bacteria – a phenomenal increase stemming from the power of repeated doubling. This rapid growth is characteristic of many natural phenomena, from population growth in ideal conditions to the spread of viral infections.
Understanding Exponential Notation: A Concise Representation
The repeated multiplication of 2 can be expressed more concisely using exponential notation. The equation 2 x 2 x 2 x 2 is equivalent to 2<sup>4</sup>, where the base (2) represents the number being multiplied and the exponent (4) represents the number of times it's multiplied by itself. This notation is crucial for dealing with larger exponents where writing out the repeated multiplication becomes cumbersome. For instance, 2<sup>10</sup> represents 2 multiplied by itself ten times, resulting in 1024.
Geometric Progressions: Visualizing Exponential Growth
The equation 2 x 2 x 2 x 2 can also be understood in terms of geometric progressions. A geometric progression is a sequence of numbers where each term after the first is found by multiplying the previous one by a constant value (the common ratio). In our case, the geometric progression is: 2, 4, 8, 16, with a common ratio of 2.
These progressions can be visualized geometrically. Imagine a square with side length 2. Its area is 2 x 2 = 4. Now imagine a cube with side length 2. Its volume is 2 x 2 x 2 = 8. Extending this to four dimensions (a hypercube), the “hypervolume” becomes 2 x 2 x 2 x 2 = 16. This visualization helps to grasp the concept of higher dimensions and the relationship between exponentiation and geometric shapes.
Beyond the Basics: Applications in Science and Technology
The concept of repeated multiplication and exponential growth, as exemplified by 2 x 2 x 2 x 2, extends far beyond basic mathematics. It plays a crucial role in various fields, including:
1. Compound Interest: The Power of Financial Growth
Compound interest is a prime example of exponential growth. Instead of earning interest only on the principal amount, you earn interest on both the principal and accumulated interest. This compounding effect leads to significant growth over time. Understanding exponential growth is crucial for making informed decisions about investments and long-term financial planning.
2. Population Dynamics: Modeling Growth and Decline
Population growth, whether of humans, animals, or bacteria, often follows exponential patterns, at least initially. Mathematical models based on exponential functions are used to predict population size, analyze resource consumption, and understand the impact of environmental factors on population dynamics. However, these models often require adjustments to account for limiting factors such as resource scarcity and competition.
3. Computer Science: Binary Numbers and Data Storage
The number 2 holds special significance in computer science due to the binary system. Computers utilize a binary system (base-2), representing information using only two digits: 0 and 1. The repeated multiplication inherent in 2 x 2 x 2 x 2 is directly related to the way data is stored and processed in computer memory. Each bit (binary digit) can represent two states, and the number of possible states increases exponentially with the number of bits. For instance, 8 bits (a byte) allow for 2<sup>8</sup> = 256 different combinations.
4. Physics: Exponential Decay and Radioactive Half-Life
While exponential growth is common, exponential decay is equally prevalent in physics. Radioactive decay follows an exponential pattern, with the amount of radioactive material decreasing by a constant fraction over time. The half-life of a radioactive substance is the time it takes for half of the material to decay, and this concept relies fundamentally on exponential decay functions.
5. Biology: Cell Division and Growth
Cell division is a process of exponential growth. A single cell divides into two, those two divide into four, and so on. This exponential proliferation is crucial for growth and development in living organisms. Understanding these exponential patterns is critical in studying cellular processes, tissue regeneration, and cancer growth.
The Philosophical Implications: Exploring Infinity and Beyond
Beyond its scientific applications, the equation 2 x 2 x 2 x 2 raises profound philosophical questions. The concept of exponential growth, when extrapolated to large numbers, points towards the concept of infinity. While we cannot physically reach infinity, the mathematical concept allows us to explore the limits of growth and the implications of unbound processes.
The repeated doubling in 2 x 2 x 2 x 2 also alludes to the potential for self-replication and the creation of complex systems from simple building blocks. This resonates with concepts of emergence, where complex patterns arise from simple underlying rules, a theme explored extensively in complexity science.
Furthermore, the equation touches upon the power of iteration and feedback loops. Each multiplication acts as a feedback mechanism, building upon the previous result. This iterative process is found in numerous natural and artificial systems, from the growth of crystals to the operation of computer algorithms.
Conclusion: Unpacking the Significance of a Simple Equation
The seemingly simple equation 2 x 2 x 2 x 2, while resulting in the straightforward answer of 16, provides a gateway to a surprisingly rich and diverse range of concepts. From the fundamentals of arithmetic to the complex dynamics of exponential growth and decay, this equation reveals its significance across diverse disciplines. Its exploration underscores the power of seemingly simple mathematical principles to unlock a deep understanding of the world around us, encompassing both the natural and artificial realms. The exploration of such fundamental equations not only enhances our mathematical literacy but also cultivates a deeper appreciation for the underlying structures governing our universe. It invites us to look beyond the immediate answer and consider the vast implications of repeated multiplication and the profound concept of exponential growth.
Latest Posts
Latest Posts
-
What Does And Mean In Spanish
Jun 15, 2025
-
Hope You Are Doing Great Reply
Jun 15, 2025
-
Vibration In Steering Wheel At High Speed
Jun 15, 2025
-
On A Vacation Or On Vacation
Jun 15, 2025
-
Sql Delete All Rows From All Tables
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 2 X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.