Write 3 3 4 As A Decimal Number
listenit
May 09, 2025 · 5 min read
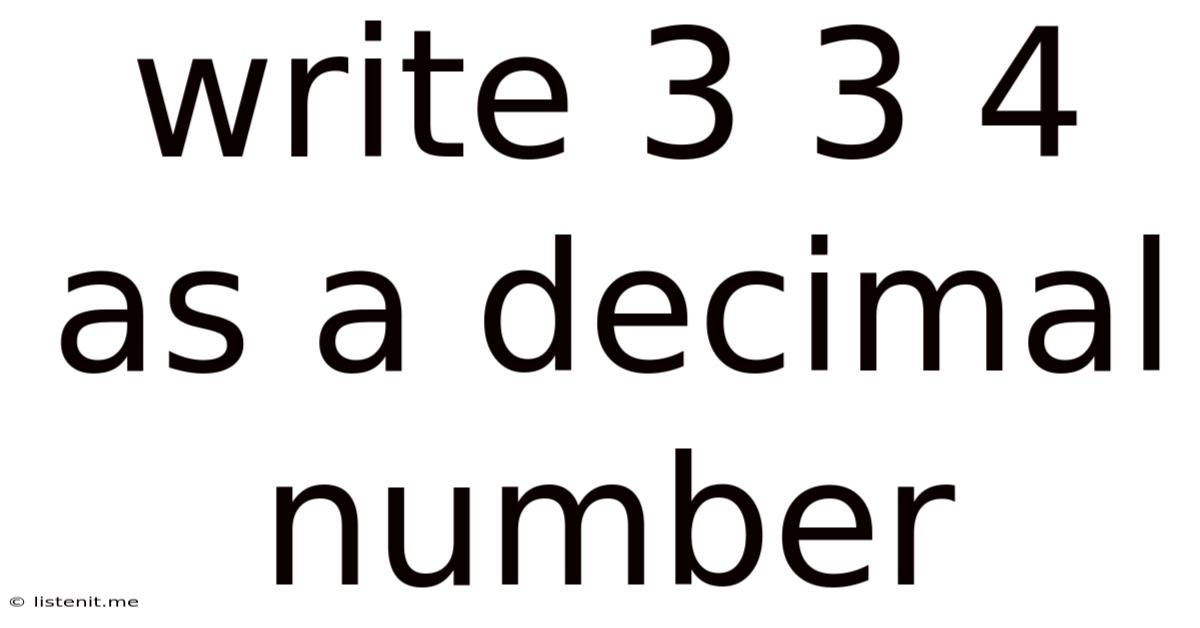
Table of Contents
Writing 3 3 4 as a Decimal Number: A Comprehensive Guide
The seemingly simple task of converting the mixed number 3 3/4 into its decimal equivalent opens a door to understanding fundamental mathematical concepts. This seemingly straightforward conversion allows us to explore different methods, each offering insights into the relationship between fractions and decimals. This comprehensive guide delves deep into this conversion, exploring multiple approaches and highlighting their underlying principles. We'll also touch upon the broader implications of understanding decimal representation and its applications in various fields.
Understanding Mixed Numbers and Decimals
Before diving into the conversion process, let's establish a clear understanding of the terms involved. A mixed number combines a whole number and a fraction, like 3 3/4. A decimal number uses a base-ten system to represent numbers, employing a decimal point to separate the whole number part from the fractional part (e.g., 3.75). The conversion process essentially involves expressing the fractional part of a mixed number as a decimal.
Method 1: Converting the Fraction to a Decimal
This is perhaps the most intuitive approach. We focus on converting the fractional part (3/4) into a decimal and then adding it to the whole number part (3).
Step 1: Divide the Numerator by the Denominator
The fraction 3/4 represents division: 3 divided by 4. Performing this division yields:
3 ÷ 4 = 0.75
Step 2: Add the Whole Number
Now, we add the whole number part (3) to the decimal equivalent of the fraction (0.75):
3 + 0.75 = 3.75
Therefore, 3 3/4 as a decimal is 3.75.
This method highlights the direct relationship between fractions and decimals – a fraction represents a division problem, and the result of that division is the decimal equivalent.
Method 2: Converting to an Improper Fraction First
This method involves an intermediate step: converting the mixed number into an improper fraction before converting it to a decimal. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert to an Improper Fraction
To convert 3 3/4 to an improper fraction, we multiply the whole number (3) by the denominator (4), add the numerator (3), and keep the same denominator (4):
(3 × 4) + 3 = 15
The improper fraction is 15/4.
Step 2: Divide the Numerator by the Denominator
Now, we divide the numerator (15) by the denominator (4):
15 ÷ 4 = 3.75
This confirms that 3 3/4 as a decimal is 3.75. This method emphasizes the equivalence between mixed numbers and improper fractions, showcasing a different path to reach the same decimal representation.
Method 3: Using Decimal Equivalents of Common Fractions
For frequently encountered fractions, such as 1/2, 1/4, 3/4, 1/5, etc., it’s beneficial to memorize their decimal equivalents. This speeds up the conversion process. Knowing that 3/4 = 0.75 allows for an immediate conversion:
3 + 0.75 = 3.75
This approach relies on memorization and recognition, making it the quickest method once the relevant decimal equivalents are known. This method is particularly useful for mental calculations and estimations.
Practical Applications and Importance
Understanding the conversion of fractions to decimals is crucial in various fields:
- Finance: Calculating percentages, interest rates, and financial ratios often requires converting fractions to decimals. For instance, understanding that a 3/4 discount is equivalent to a 0.75 or 75% discount is vital.
- Engineering and Science: Many engineering and scientific calculations utilize decimals extensively. Converting measurements from fractions to decimals ensures consistent and accurate calculations.
- Cooking and Baking: Precise measurements are critical in cooking and baking. Converting fractional measurements to decimals enables greater accuracy.
- Data Analysis: In statistical analysis and data representation, using decimals facilitates calculations and clear visualization of data.
- Everyday Life: From calculating tips to understanding sales discounts, the ability to convert fractions to decimals is a practical skill applicable to numerous everyday situations.
Beyond 3 3/4: Expanding the Concept
The techniques discussed for converting 3 3/4 to a decimal are applicable to converting any mixed number. The fundamental principles – dividing the numerator by the denominator and adding the whole number – remain consistent. For example:
- 2 1/2: 1/2 = 0.5; 2 + 0.5 = 2.5
- 5 2/5: 2/5 = 0.4; 5 + 0.4 = 5.4
- 1 7/8: 7/8 = 0.875; 1 + 0.875 = 1.875
Mastering the conversion of mixed numbers to decimals strengthens your understanding of fractional and decimal representation, which are essential building blocks in various mathematical and real-world applications. It's a seemingly simple conversion, yet it provides a strong foundation for more complex mathematical concepts and problem-solving.
Troubleshooting Common Errors
While the conversion process is relatively straightforward, common errors can arise:
- Incorrect division: Ensure accurate division of the numerator by the denominator. Using a calculator can help minimize errors, but understanding the division process is crucial.
- Forgetting the whole number: Remember to add the whole number to the decimal equivalent of the fraction.
- Improper fraction errors: When using the improper fraction method, double-check the conversion to ensure the improper fraction is calculated correctly.
Conclusion: Mastering Decimal Conversions
The conversion of 3 3/4 to 3.75, while seemingly simple, opens a window into the fundamental interplay between fractions and decimals. By exploring multiple methods, understanding the underlying principles, and recognizing the practical applications, we gain a deeper appreciation for this core mathematical concept. This understanding enhances problem-solving skills, improves accuracy in calculations, and broadens our ability to tackle more complex mathematical challenges across various disciplines. The ability to seamlessly translate between fractions and decimals is a versatile skill that extends beyond the classroom and into the practical realities of everyday life and specialized fields.
Latest Posts
Latest Posts
-
How To Factor X 2 2
May 11, 2025
-
3x 2y 10 In Slope Intercept Form
May 11, 2025
-
What Is The Fraction For 2 25
May 11, 2025
-
Common Factors Of 20 And 35
May 11, 2025
-
The Part Of The Pistil That Receives The Pollen
May 11, 2025
Related Post
Thank you for visiting our website which covers about Write 3 3 4 As A Decimal Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.