Why Is The Integral Of 1/x Ln X
listenit
May 12, 2025 · 5 min read
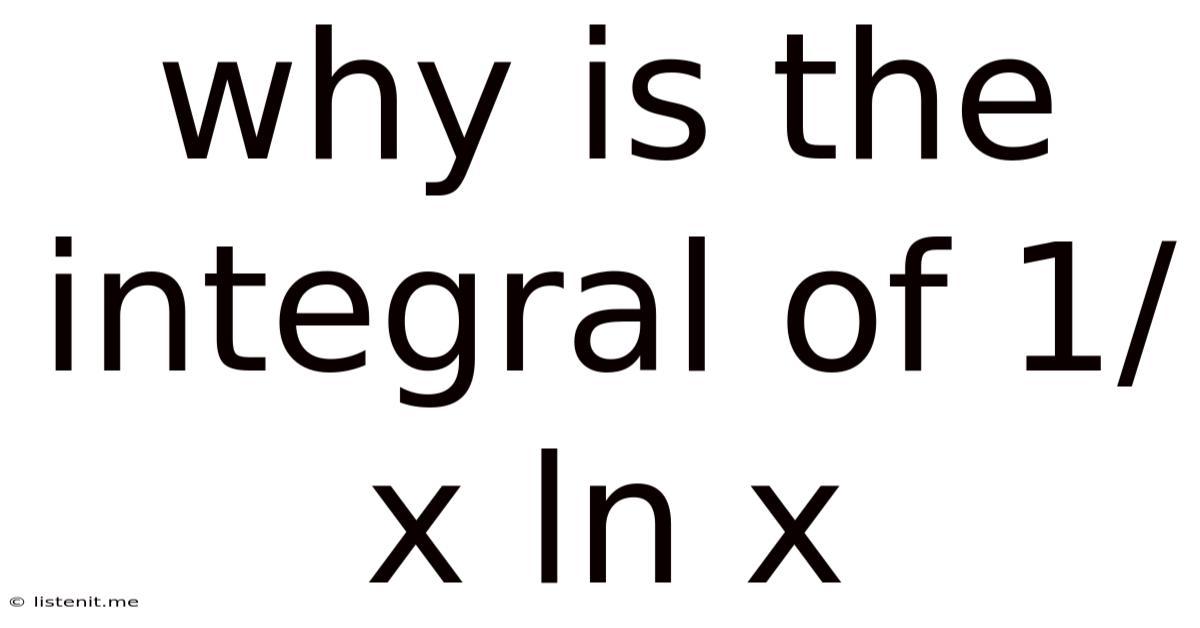
Table of Contents
Why is the Integral of 1/x ln|x|? A Deep Dive into Logarithmic Integration
The integral of 1/x is a fundamental concept in calculus, often causing confusion for students new to the subject. While the result, ln|x| + C (where C is the constant of integration), seems deceptively simple, understanding why this is the case requires a deeper exploration of logarithmic properties, differentiation, and the very definition of the integral. This article will delve into the intricacies of this integral, providing a comprehensive explanation supported by examples and addressing common misconceptions.
Understanding the Integral as the Inverse of Differentiation
The cornerstone of understanding this integral lies in recognizing the integral as the inverse operation of differentiation. If the derivative of a function f(x) is g(x), then the integral of g(x) is f(x) (plus the constant of integration). This inverse relationship is crucial.
Let's consider the derivative of the natural logarithm function, ln(x):
The Derivative of ln(x)
The derivative of ln(x) with respect to x is given by:
d/dx [ln(x)] = 1/x (for x > 0)
This is a fundamental result derived from the definition of the derivative and the properties of exponential and logarithmic functions. The proof often involves using the definition of the derivative as a limit, the properties of exponentials, and L'Hôpital's rule. However, for our purposes, we accept this as a given.
The Integral of 1/x: The Inverse Operation
Since the derivative of ln(x) is 1/x, the antiderivative (or indefinite integral) of 1/x must be ln(x). This is the core logic behind the solution. The integral of 1/x represents the family of functions whose derivative is 1/x.
∫ (1/x) dx = ln|x| + C
Notice the addition of the absolute value sign, |x|, and the constant of integration, C. Let's explore why these are crucial:
The Importance of the Absolute Value |x|
The absolute value is included because the natural logarithm function, ln(x), is only defined for positive values of x. However, the function 1/x is defined for all x except x=0. To account for negative values of x, we incorporate the absolute value.
Consider the function f(x) = ln|x|. Its derivative is:
- For x > 0: d/dx [ln(x)] = 1/x
- For x < 0: d/dx [ln(-x)] = (1/(-x)) * (-1) = 1/x (using the chain rule)
Thus, the derivative of ln|x| is 1/x for all x ≠ 0, justifying the use of the absolute value in the integral. Without it, the integral wouldn't be defined for negative x values.
The Constant of Integration, C
The constant of integration, C, is essential because the derivative of a constant is always zero. Therefore, any constant can be added to ln|x| and still yield a derivative of 1/x. For example, the derivative of ln|x| + 5, ln|x| - 2, or ln|x| + π is still 1/x.
The constant C represents the family of curves that all have the same derivative. Determining the specific value of C requires additional information, usually in the form of an initial condition or boundary condition.
Exploring Related Integrals and Applications
The integral of 1/x forms the basis for understanding many other integrals and has significant applications in various fields:
Integrals Involving Logarithmic Expressions
Many integrals involving logarithmic functions can be solved using substitution and integration by parts, often leading back to the fundamental integral of 1/x. For example:
Example 1: ∫ (ln(x)/x) dx
This can be solved using the substitution u = ln(x), du = (1/x)dx. This transforms the integral to ∫ u du, which easily integrates to (1/2)u² + C. Substituting back u = ln(x), the solution becomes (1/2)(ln(x))² + C.
Example 2: ∫ (1/(xlnx)) dx
Here, the substitution u = ln(x), du = (1/x)dx simplifies the integral to ∫(1/u)du = ln|u| + C = ln|ln|x|| + C (for x>0). Note the double absolute value.
Applications in Various Fields
The integral of 1/x and its logarithmic solution have crucial applications in numerous fields including:
- Physics: Calculating work done by expanding gases, solving differential equations in various physical phenomena.
- Chemistry: Determining reaction rates and concentrations in chemical kinetics.
- Finance: Modeling continuous growth and decay processes, calculating compound interest.
- Computer Science: Analysis of algorithms and data structures, especially those involving logarithmic time complexity.
Addressing Common Misconceptions
Several common misunderstandings surrounding this integral need clarification:
-
Confusion with the Power Rule: The power rule of integration, ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, does not apply when n = -1. This is because the power rule involves division by (n+1), which is undefined when n = -1.
-
Ignoring the Absolute Value: Omitting the absolute value sign |x| is a significant error as it restricts the domain of the solution to positive values of x only.
-
Forgetting the Constant of Integration: Leaving out the constant of integration, C, is incomplete and doesn't represent the entire family of functions whose derivatives are 1/x.
Conclusion
The integral of 1/x being ln|x| + C is not just a formula to memorize; it’s a direct consequence of the inverse relationship between differentiation and integration, coupled with the properties of the natural logarithm. Understanding this relationship, including the roles of the absolute value and the constant of integration, is vital for mastering logarithmic integration and its wide-ranging applications. The examples and clarifications provided in this article aim to provide a complete and intuitive understanding of this crucial concept. Through careful consideration of both the mathematical derivation and its practical application, a more profound understanding can be attained. This detailed explanation hopefully demystifies the integral of 1/x, solidifying your grasp of calculus and preparing you to tackle more complex logarithmic problems with confidence.
Latest Posts
Latest Posts
-
Bromine Has How Many Valence Electrons
May 13, 2025
-
What Is The Function Of Electrons
May 13, 2025
-
What Unit Does A Graduated Cylinder Measure
May 13, 2025
-
The Amount Of Matter In A Substance
May 13, 2025
-
Does Rate Constant Increase With Temperature
May 13, 2025
Related Post
Thank you for visiting our website which covers about Why Is The Integral Of 1/x Ln X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.