Which Is The Factorization Of X3 8
listenit
May 09, 2025 · 4 min read
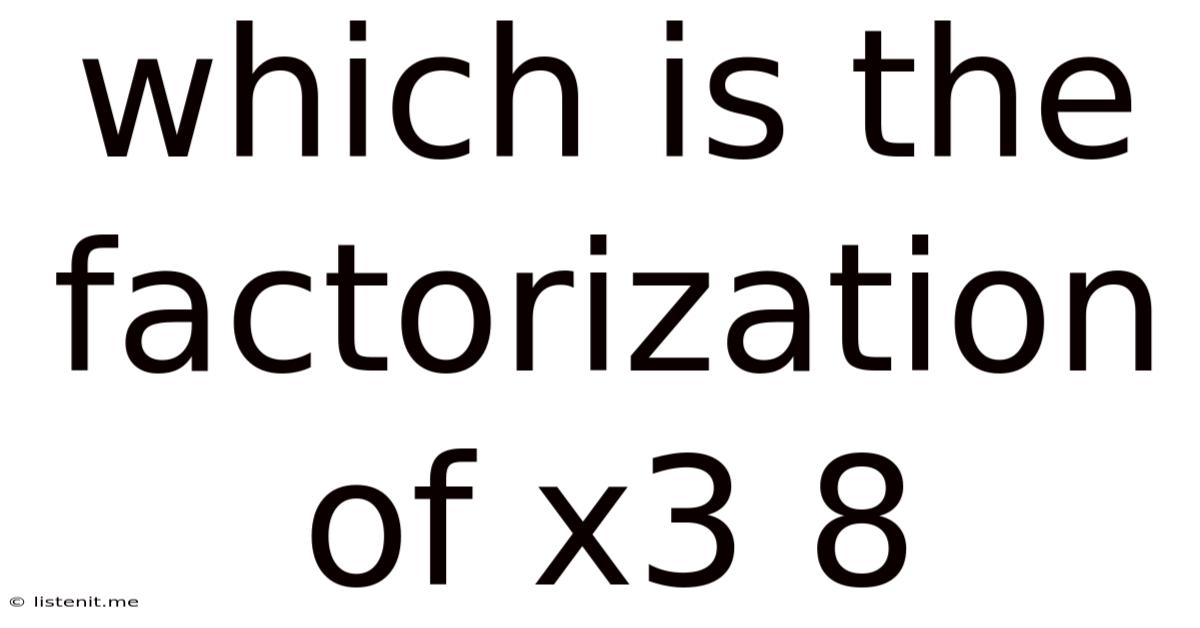
Table of Contents
Factoring x³ + 8: A Comprehensive Guide
The expression x³ + 8 might seem simple at first glance, but understanding its factorization reveals a deeper understanding of algebraic manipulation and its applications. This comprehensive guide will explore the various methods of factoring x³ + 8, delving into the underlying mathematical principles and showcasing practical applications. We'll go beyond simply providing the answer; we'll equip you with the knowledge to tackle similar cubic expressions with confidence.
Understanding the Sum of Cubes Formula
The key to factoring x³ + 8 lies in recognizing it as a sum of cubes. This specific form, a³ + b³, has a well-defined factorization:
a³ + b³ = (a + b)(a² - ab + b²)
In our case, x³ + 8 can be rewritten as:
x³ + 2³
Here, 'a' is x and 'b' is 2. Therefore, applying the sum of cubes formula, we get:
x³ + 8 = (x + 2)(x² - 2x + 4)
This is the complete factorization of x³ + 8. Let's break down why this formula works and explore alternative approaches to arrive at the same result.
Deriving the Sum of Cubes Formula
While the formula itself is readily available, understanding its derivation enhances comprehension. We can derive it through polynomial long division or by expanding the factored form. Let's explore the expansion method:
(a + b)(a² - ab + b²) = a(a² - ab + b²) + b(a² - ab + b²)
Expanding further:
= a³ - a²b + ab² + a²b - ab² + b³
Notice that several terms cancel each other out (-a²b and +a²b, +ab² and -ab²). This leaves us with:
= a³ + b³
This confirms the validity of the sum of cubes factorization formula.
Alternative Methods for Factoring x³ + 8
While the sum of cubes formula is the most direct and efficient approach, let's consider alternative methods, which might be helpful in understanding the underlying concepts or in dealing with more complex scenarios.
Method 1: Polynomial Long Division
If you didn't recognize the sum of cubes pattern immediately, polynomial long division could be used. We know that (x + 2) is a factor because -2 is a root of x³ + 8 (since (-2)³ + 8 = 0). Performing polynomial long division with (x + 2) as the divisor would yield the quadratic factor (x² - 2x + 4).
Method 2: Factoring by Grouping (Not Directly Applicable Here)
Factoring by grouping is a technique often used for polynomials with four or more terms. It's not directly applicable to x³ + 8, which only has two terms. However, understanding this method is valuable for factoring more complex polynomials.
Analyzing the Quadratic Factor (x² - 2x + 4)
The complete factorization of x³ + 8 is (x + 2)(x² - 2x + 4). Let's investigate the quadratic factor (x² - 2x + 4). This quadratic expression doesn't factor further using real numbers. To find its roots, we would employ the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Where a = 1, b = -2, and c = 4. Substituting these values:
x = [2 ± √((-2)² - 4 * 1 * 4)] / 2 * 1
x = [2 ± √(-12)] / 2
x = [2 ± 2i√3] / 2
x = 1 ± i√3
This reveals that the quadratic factor has two complex conjugate roots (1 + i√3 and 1 - i√3). This is a common characteristic when factoring cubic equations; they may have a combination of real and complex roots.
Applications of Factoring Cubic Expressions
Factoring cubic expressions, such as x³ + 8, is not just a theoretical exercise; it has significant applications in various fields:
1. Calculus: Finding Derivatives and Integrals
In calculus, factoring can simplify the process of finding derivatives and integrals. A factored form often allows for easier application of differentiation and integration rules.
2. Engineering and Physics: Solving Equations
Cubic equations frequently arise in solving problems in engineering and physics, such as determining the stability of structures, analyzing circuits, or modeling physical phenomena. Factoring helps find the solutions to these equations, which are crucial for design and analysis.
3. Computer Science: Algorithm Design and Optimization
Factoring polynomials is fundamental in computational algebra and algorithm design. Efficient factoring algorithms play a role in cryptography and various optimization problems.
4. Economics and Finance: Modeling Growth and Decay
Cubic functions can model growth and decay processes in economics and finance. Factoring the resulting equations can help analyze equilibrium points and predict future trends.
Further Exploration: Difference of Cubes and Beyond
While we've focused on the sum of cubes, there's also a corresponding formula for the difference of cubes:
a³ - b³ = (a - b)(a² + ab + b²)
This formula is similarly valuable for factoring expressions of the form a³ - b³.
Moving beyond cubic expressions, factoring higher-degree polynomials can become considerably more complex. Techniques such as the Rational Root Theorem and numerical methods are employed for such higher-degree polynomials.
Conclusion: Mastering Polynomial Factorization
Factoring x³ + 8, as a specific example of a sum of cubes, demonstrates the importance of understanding fundamental algebraic concepts and applying factorization techniques. The ability to factor polynomials is crucial for various applications across multiple disciplines, from calculus and engineering to computer science and economics. Mastering these techniques not only enhances mathematical skills but also equips you with problem-solving capabilities valuable in a wide range of fields. By understanding the sum of cubes formula, exploring alternative methods, and analyzing the resulting factors, you gain a deeper appreciation for the elegance and practicality of algebraic manipulation.
Latest Posts
Latest Posts
-
Why Is High Specific Heat Important To Life
May 09, 2025
-
4x 2y 6 In Slope Intercept Form
May 09, 2025
-
Definition Of Converse Of The Pythagorean Theorem
May 09, 2025
-
What Temperature Does Water Freeze In Kelvin
May 09, 2025
-
Equation Of A Line That Is Parallel To
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Factorization Of X3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.