Which Fractions Are Equivalent To 3 4
listenit
Apr 03, 2025 · 5 min read
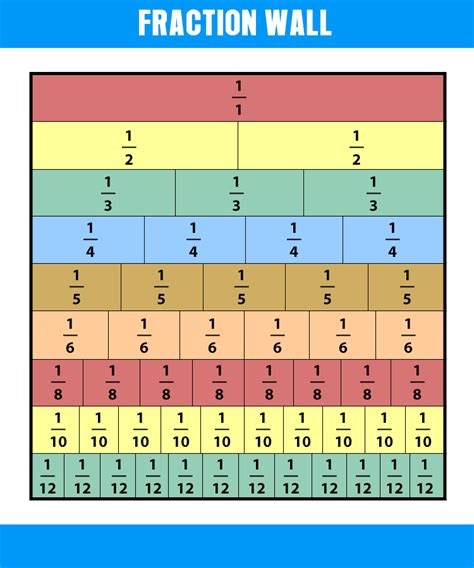
Table of Contents
Which Fractions Are Equivalent to 3/4? A Comprehensive Guide
Finding equivalent fractions can seem daunting, especially when you're dealing with mixed numbers like 3/4. But understanding the underlying principle – that equivalent fractions represent the same portion of a whole – simplifies the process immensely. This comprehensive guide will explore various methods to identify fractions equivalent to 3/4, covering fundamental concepts and advanced techniques. We'll also examine the practical applications of understanding equivalent fractions and how this knowledge benefits mathematical problem-solving.
Understanding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same value despite having different numerators and denominators. The key to creating equivalent fractions is the principle of multiplying or dividing both the numerator and the denominator by the same non-zero number. This maintains the ratio between the numerator and the denominator, ensuring the fraction retains its original value.
For example, consider the fraction 1/2. If we multiply both the numerator and the denominator by 2, we get 2/4. Similarly, multiplying by 3 yields 3/6, by 4 yields 4/8, and so on. All these fractions—1/2, 2/4, 3/6, 4/8—are equivalent because they all represent one-half of a whole.
This principle forms the bedrock of finding fractions equivalent to 3/4.
Methods for Finding Equivalent Fractions of 3/4
Several methods effectively generate equivalent fractions for 3/4. Let's explore the most common and practical approaches:
1. Multiplication Method: The Simplest Approach
The most straightforward method involves multiplying both the numerator (3) and the denominator (4) by the same whole number. This creates an infinite set of equivalent fractions:
- Multiply by 2: (3 x 2) / (4 x 2) = 6/8
- Multiply by 3: (3 x 3) / (4 x 3) = 9/12
- Multiply by 4: (3 x 4) / (4 x 4) = 12/16
- Multiply by 5: (3 x 5) / (4 x 5) = 15/20
- Multiply by 10: (3 x 10) / (4 x 10) = 30/40
- Multiply by 100: (3 x 100) / (4 x 100) = 300/400
And so on. You can continue this process indefinitely, generating an endless sequence of equivalent fractions. This illustrates that there are infinitely many fractions equivalent to 3/4.
2. Division Method: Simplifying Fractions
While multiplication generates larger equivalent fractions, division simplifies them to their lowest terms. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by it. For example, consider the fraction 12/16. The GCD of 12 and 16 is 4. Dividing both the numerator and denominator by 4 yields 3/4, the simplest form of the fraction. This process works in reverse as well – starting with 3/4, you can multiply to get 12/16, which you can then simplify back to 3/4 by dividing by the GCD.
3. Using a Common Multiple: A Systematic Approach
Another approach involves finding a common multiple of the denominator (4). Let's say we choose 20 as a common multiple of 4 (4 x 5 = 20). To find the equivalent fraction with a denominator of 20, we set up a proportion:
3/4 = x/20
Solving for x:
x = (3 x 20) / 4 = 15
Therefore, 15/20 is an equivalent fraction to 3/4. This method works for any common multiple of the denominator.
Visualizing Equivalent Fractions: A Geometrical Approach
Visual aids enhance understanding. Imagine a circle divided into four equal parts. Shading three of those parts represents the fraction 3/4. Now, imagine dividing the same circle into eight equal parts. Shading six of those parts still represents the same area, illustrating that 6/8 is equivalent to 3/4. This geometric representation can be extended to other equivalent fractions, solidifying the concept visually.
The Importance of Equivalent Fractions
Understanding and working with equivalent fractions is fundamental to various mathematical concepts and applications:
1. Simplifying Fractions: Reducing to Lowest Terms
Simplifying fractions to their lowest terms is essential for easier calculations and clearer representation of values. Finding equivalent fractions allows us to reduce complex fractions to their simplest form.
2. Comparing Fractions: Determining Greater or Lesser Values
Comparing fractions becomes easier when they share a common denominator. Finding equivalent fractions with a common denominator enables straightforward comparison to determine which fraction holds a greater or lesser value.
3. Adding and Subtracting Fractions: Finding a Common Denominator
Adding and subtracting fractions require a common denominator. Finding equivalent fractions that share a common denominator is a crucial step in performing these arithmetic operations.
4. Solving Equations: Manipulating Fractions
Solving equations involving fractions often necessitates finding equivalent fractions to simplify the equation and isolate the variable.
5. Real-World Applications: Proportions and Ratios
Equivalent fractions are vital in understanding and solving real-world problems involving proportions and ratios. For example, scaling recipes, calculating percentages, and determining proportions in mixtures all utilize the concept of equivalent fractions.
Advanced Techniques and Considerations
1. Decimal Representation: Connecting Fractions and Decimals
The fraction 3/4 can also be expressed as a decimal: 0.75. Any fraction equivalent to 3/4 will also have a decimal representation of 0.75. This connection highlights the different ways to represent the same numerical value.
2. Percentage Representation: Expressing Fractions as Percentages
The fraction 3/4 is equivalent to 75% (3/4 x 100%). Any equivalent fraction will also represent 75% of a whole.
3. Improper Fractions and Mixed Numbers: Expanding the Scope
While we've primarily focused on the fraction 3/4, the principles apply equally to improper fractions and mixed numbers. For instance, 15/4 is an improper fraction equivalent to 3 3/4, which further exemplifies the concept of representing the same value differently.
Conclusion: Mastering Equivalent Fractions
Mastering the concept of equivalent fractions is crucial for success in mathematics. Understanding how to find and utilize equivalent fractions simplifies various mathematical operations, from simplifying fractions and comparing values to adding, subtracting, and solving equations. By utilizing the methods outlined – multiplication, division, and finding common multiples – you can confidently generate an infinite number of fractions equivalent to 3/4, strengthening your understanding of fundamental mathematical principles and their real-world applications. Remember, visual aids and real-world examples can significantly improve your grasp of this important concept. The ability to recognize and work with equivalent fractions is a cornerstone of mathematical proficiency and opens doors to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
5 X 4 25 X 6
Apr 04, 2025
-
What Shape Is Not A Parallelogram
Apr 04, 2025
-
What Is The Ultimate Source Of Energy In An Ecosystem
Apr 04, 2025
-
What Is The Prime Factorization For 44
Apr 04, 2025
-
Why Did Conservatives Oppose The New Deal
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Which Fractions Are Equivalent To 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
