Whats The Square Root Of 125
listenit
Apr 02, 2025 · 5 min read
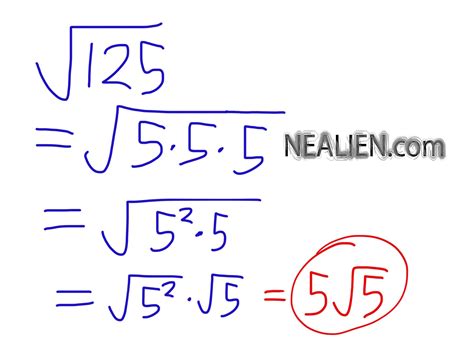
Table of Contents
What's the Square Root of 125? A Deep Dive into Square Roots and Simplification
Finding the square root of 125 might seem like a simple mathematical problem, but it opens the door to understanding fundamental concepts in algebra and number theory. This article delves into the process of calculating the square root of 125, exploring various methods, explaining the concept of simplifying radicals, and showcasing the practical applications of this seemingly simple calculation.
Understanding Square Roots
Before we tackle the square root of 125, let's establish a firm understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. This can be represented mathematically as √9 = 3.
The square root symbol (√) is also known as a radical symbol. The number inside the radical symbol is called the radicand. In our case, the radicand is 125.
Calculating the Square Root of 125
Unlike the square root of a perfect square (like 9, 16, 25, etc.), the square root of 125 is not a whole number. It's an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. However, we can simplify it.
The key to simplifying the square root of 125 lies in finding its prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's break down 125 into its prime factors:
125 = 5 x 25 = 5 x 5 x 5 = 5³
Now, we can rewrite the square root of 125 using this prime factorization:
√125 = √(5 x 5 x 5) = √(5² x 5)
Remember that √(a x a) = a. Therefore, we can simplify:
√(5² x 5) = √5² x √5 = 5√5
Therefore, the simplified form of the square root of 125 is 5√5.
This is the exact value. To obtain an approximate decimal value, you can use a calculator:
5√5 ≈ 5 x 2.236 ≈ 11.18
Methods for Calculating Square Roots
While we've focused on simplifying the square root of 125 using prime factorization, several other methods exist for calculating square roots, both approximate and precise:
1. Prime Factorization (as shown above)
This method is particularly useful for simplifying radicals and understanding the structure of the number. It provides the exact answer in its simplest form.
2. Using a Calculator
Calculators provide a quick and easy way to obtain an approximate decimal value for the square root of any number. Simply input 125 and press the square root button (√).
3. Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations of a square root. It's based on the principle of repeatedly averaging a guess with the result of dividing the number by the guess. While more complex than using a calculator, it's a fascinating example of an ancient numerical algorithm.
4. Long Division Method
This method, while lengthy, allows for manual calculation of the square root to a desired level of accuracy. It involves a series of steps similar to long division but specific to square root calculation. It's less practical than other methods in the modern age of readily available calculators.
Applications of Square Roots
Understanding square roots isn't just an academic exercise; it has numerous practical applications across various fields:
1. Geometry and Trigonometry
Square roots are fundamental in geometry, particularly in calculating distances, areas, and volumes. The Pythagorean theorem (a² + b² = c²) heavily relies on square roots to find the length of the hypotenuse of a right-angled triangle. Trigonometric functions also frequently involve square roots.
2. Physics and Engineering
Many physics equations, especially those dealing with motion, energy, and forces, involve square roots. For example, calculating the velocity of an object based on its kinetic energy requires the use of a square root. Similarly, engineering problems related to structural stability and dynamics often involve square root calculations.
3. Statistics and Probability
Standard deviation, a crucial concept in statistics, involves calculating the square root of the variance. Understanding standard deviation is vital for analyzing data and making informed decisions in various fields, including finance, healthcare, and social sciences.
4. Computer Graphics and Game Development
Square roots are crucial for vector calculations and coordinate transformations in computer graphics and game development. These calculations are essential for rendering images, handling movement and collisions, and creating realistic simulations.
5. Finance and Investment
Square roots play a role in calculating portfolio volatility, option pricing, and other financial models. These calculations help investors assess risk and manage their investments effectively.
Beyond the Square Root of 125: Exploring Other Radicals
While this article focused on the square root of 125, the concepts discussed extend to other radicals, such as cube roots (∛), fourth roots (∜), and so on. These higher-order roots follow similar principles of prime factorization and simplification.
Conclusion
The seemingly simple question, "What's the square root of 125?" has led us on a journey through the world of square roots, radical simplification, and various calculation methods. We've seen that the answer, 5√5, represents not just a numerical value but also a fundamental concept with far-reaching implications across numerous disciplines. Understanding square roots and the associated mathematical principles is crucial for navigating complex problems in various fields and developing a strong foundation in mathematics and its applications. From the Pythagorean theorem to advanced statistical analysis, the square root of 125, and the broader concept of square roots, serves as a cornerstone of mathematical understanding and practical application.
Latest Posts
Latest Posts
-
How Much 70 Fahrenheit In Celsius
Apr 03, 2025
-
All Living Things Are Made Of What
Apr 03, 2025
-
The Movement Of Water Through A Selectively Permeable Membrane
Apr 03, 2025
-
What Percent Is 3 Out Of 20
Apr 03, 2025
-
500 Ml Of Water Is How Many Ounces
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
